Perkalian vektor ada 2 macam yaitu perkalian dot(dot product) dan perkalian cross(cross product). Perkalian dot menghasilkan skalar sedangkan perkalian cross menghasilkan vektor
A. Perkalian Dot(Perkalian titik)
Misalkan terdapat vektor A = Axi + Ayj + Azk dan vektor B = Bxi + Byj + Bzk
kedua vektor tersebut dapat dihitung dengan menggunakan perkalian dot seperti berikut:
A.B=AxBx+AyBy+AzBz
atau
A.B = ABcosθ
Sudut antara 2 vektor A.B
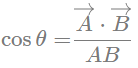
B. Perkalian Cross (perkalian silang)
Perkalian silang vektor dapat diperoleh melalui persamaan di bawah ini

C. Contoh Soal
Soal.01
Hitunglah operasi perkalian vektor F.X Jika F = 3i − 4j + 6k dan X= −7i + 5j − 8k Sudut antara 2 vektor adalah θ=165.9374047
Jawab.01
F⋅X = FxXx + FyXy + FzXz
= (3)(−7) + (−4)(5) +(6)(−8)
= −89
Cara Lain

Soal.02
Diketahui vektor A = 9i + 5j − 3k dan B = −4i + 6j − 7k . Tentukan hasil perkalian vektor dari A→×B→A×B.
Jawab.02
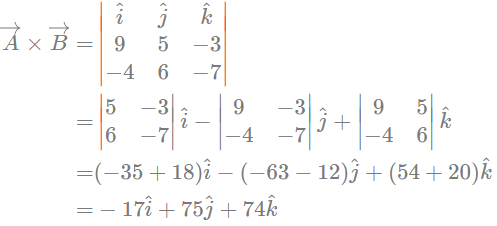

Leave a Reply