
A. Identitas trigonometri Dasar
- Identitas trigonometri merupakan pernyataan yang memuat kesamaan dua bentuk untuk setiap penggantian variabelnya dengan nilai di mana bentuk tersebut didefinisikan.
- Jadi identitas trigonometri terjadi Jika Terdapat dua fungsi trigonometri atau lebih yang memiliki bentuk berbeda, tetapi grafik fungsinya sama.
Contoh, dua fungsi :
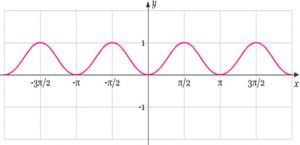
Kedua fungsi tersebut jika digambar grafik akan mempunyai fungsi yang sama:
Kedua fungsi tersebut memiliki grafik yang sama maka dapat disebut sebagai fungsi identitas sehingga dapat ditulis :
B. Rumus dasar Identitas Trigonometri
Kotak warna orange disebut sebagai identitas kebalikan.
kotak warna hijau disebut sebagai identitas rasio.
Kotak berwarna biru disebut sebagai identitas Pythagoras
C. Cara menyelesaikan Idendtitas Trigonometri
- Manipulasi ruas persamaan yang lebih rumit terlebih dahulu.
- Carilah bentuk yang dapat disubstitusi dengan bentuk trigonometri yang ada dalam identitas trigonometri, sehingga didapatkan bentuk yang lebih sederhana.
- Perhatikan operasi-operasi aljabar, seperti penjumlahan pecahan, sifat distributif, atau pemfaktoran, yang mungkin dapat menyederhanakan ruas yang kita manipulasi, atau minimal dapat membimbing kita kepada bentuk yang dapat disederhanakan.
- Jika kita tidak tahu apa yang harus dilakukan, ubahlah semua bentuk trigonometri menjadi bentuk sinus dan cosinus. Mungkin hal tersebut bisa membantu.
- Selalu perhatikan ruas persamaan yang tidak kita manipulasi untuk memastikan langkah-langkah yang kita lakukan menuju bentuk dalam ruas tersebut.
D. Contoh Soal
Soal 1
Buktikan bahwa sin θ cot θ = cos θ.
Soal 2
Sederhanakan bentuk trigonometri (1 + cot2 β) / (cot β . sec2 β)
Pembahasan 2
1 + cot2 β = cosec2 β
⇒ 1 + cot2 β = 1/sin2 β
cot β . sec2 β = (cos β/ sinβ) . sec2 β
⇒ cot β . sec2 β = (cos β/ sin β).(1/cos2 β)
⇒ cot β . sec2 β = cos β / sin β.cos2 β
Setelah digabung kembali diperoleh :
(1 + cot2 β) / (cot β . sec2 β) = (1/sin2 β) / (cos β / sinβ.cos2 β)
⇒ (1 + cot2 β) / (cot β . sec2 β) = (1/sin2 β) . (sin β.cos2 β / cos β)
⇒ (1 + cot2 β) / (cot β . sec2 β) = sin β.cos2 β / sin2 β.cos β
⇒ (1 + cot2 β) / (cot β . sec2 β) = cos β / sin β
⇒ (1 + cot2 β) / (cot β . sec2 β) = cot β
Jadi, (1 + cot2 β) / (cot β . sec2 β) = cot β.
Soal 3
Tentukan nilai dari (sin α – cos α)2 + 2 sin α cos α.
Karena keterbatasan ruang dan pengkodean, jadi soal di atas dikerjakan masing-masing agar tidak terlalu panjang.
(sin α – cos α)2 = sin2 α – 2 sin α. cos α + cos2 α
⇒ (sin α – cos α)2 = sin2 α + cos2 α – 2 sin α. cos α
⇒ (sin α – cos α)2 = 1 – 2 sin α. cos α
(sin α – cos α)2 + 2 sin α cos α = 1 – 2 sin α. cos α + 2 sin α cos α
⇒ (sin α – cos α)2 + 2 sin α cos α = 1
Jadi, (sin α – cos α)2 + 2 sin α cos α = 1.
Buktikan bahwa sec4 α – sec2 α = tan4 α + tan2 α
sec4 α – sec2 α = tan4 α + tan2 α
⇒ sec2 α (sec2 α – 1) = tan2 α (tan2 α + 1)
⇒ sec2 α (tan2 α) = tan2 α (sec2 α)
⇒ sec2 α . tan2 α = sec2 α . tan2 α
Jadi, sec4 α – sec2 α = tan4 α + tan2 α = sec2 α . tan2 α.
Terbukti.

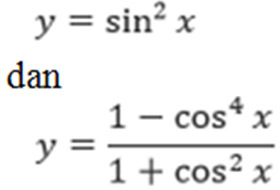


Leave a Reply