
A. Pengertian Teorema Sisa dan Teorema Faktor
- Suku banyak atau Polinom terbagi menjadi dua bagian utama yaitu teorema sisa dan teorema faktor
- Suku banyak (polinomial) Adalah sebuah ungkapan aljabar Yang variabel (peubahnya) berpangkat Bilangan bulat non
negative. - Teorema Sisa merupakan sisa pembagian suku banyak
- Jika terdapat suku banyak f(x)
dibagi (x – a), maka sisanya f(a)
dibagi (x + a), maka sisanya f(-a)
dibagi (ax – b), maka sisanya f(b/a) - Teorema Faktor, Jika f(x) adalah suku banyak, (x – k) merupakan faktor dari P(x), jika dan hanya jika P(k) = 0
- Dengan kata lain “Suatu pembagi suku banyak disebut faktor jika hasilnya nol(0), atau tidak memiliki sisa”
B. Pembahasan Teorema sisa
- Tentukan sisanya jika 2x3 – x2 + 7x + 6 dibagi x + 1 dengan menggunakan teorema sisa dan buktikan
Pembahasan
Dengan menggunakan teorema sisa
P(-1) = 2.(-1)3 – (-1)2 + 7(-1) + 6
= – 2 – 1 – 7 + 6
= -4
Pembuktian
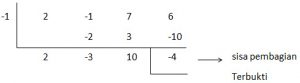
C. Teorema Faktor
- Tunjukan (x + 1) faktor dari x3 + 4x2 + 2x – 1
Pembahasan
(x + 1) faktornya, berarti P(-1) = 0
P(-1) = (-1)3 + 4(-1)2 + 2(-1) – 1
= -1 + 4 – 2 – 1 = 0 –> sisa 0
Pembuktian

Karena Sisa pembagiannya 0 maka (x-1) merupakan faktor dari x3 + 4x2 + 2x – 1
D. Soal Latihan
- x3 – 3x + 6 dibagi (x + 2) dengan teorema sisa, buktikan
- Tentukan Sisa pembagian f(x) = 4x5 + 3x3 + x +4 dibagi (2x + 1) buktikan
- Suku banyak f(x) Jika dibagi (x – 1) sisanya 3 jika dibagi (x – 2) sisanya 4 Jika f(x) dibagi dengan (x2 – 3x + 2) maka tentukan sisanya…..
- Suku banyak f(x) memiliki sisa (x + 3) jika dibagi (x2 – 4). Sedang saat dibagi (x2 + 3x + 2) memeiliki hasil bagi (x2 – 2x) tentukan persamaan f(x) nya…
- Suku banyak f(x) = x4 + 3x3 + x2 − (p + x) + 1 dibagi dengan x – 2 memberikan sisa = 35. Tentukan nilai p
- Tentukan nilai k sehingga (x + 3a) merupakan faktor dari x3 + ( ak + 2a)x2 + 18a3
- Tunjukkan bahwa (x + 5) adalah faktor dari x3 + 4x2 + 11x + 30
- Tentukan faktor-faktor dari P(x) = 2x3 – x2 – 7x + 6
- Diketahui (x – 2) adalah faktor, P(x) = 2x3 + x2 + ax – 6, Tentukan faktor lainnya
- Sukubanyak f(x) = x3 – ax2 + bx – 2 mempunyai faktor (x – 1). Jika dibagi oleh (x + 2) bersisa -36, maka nilai a + b adalah….

5)
Dik:F(x)=x^4+3x^2+x^2-(p+x)+1 dibagi (x-2) mempunyai sisa 35
Dit:p?
Jwb:
Dibagi (x-2),maka f(2)
F(2)»x^4+3x^2+x^2-(p+x)+1=35
»2^4+3(2)^2+2^2-(p+2)+1=35
»16+12+4.(p+2)+1=35
»45-p-2=35
»43-p=35
»43-35=p
»8=p
Jadi,nilai p adalah 8
2)
dik:f(x)=4x^5+3x^3+x+4
dit:tentukan sisa pembagian jika dibagi (2x+1) dan buktikan.
Jwb:
Dibagi (ax+b),maka sisanya f(-b/a)
F(-1/2)=4(-1/2)^5+3(-1/2)^3+(-1/2)+4
=4(-1/32)+3(-1/8)+(-1/2)+4
=-1/8+(-3/8)+(-1/2)+4 =3
Pembuktian
»Metode Horner
-1/2|4 0 3 0 1 4
| -2 1 -2 1 -1
__________________
4 -2 4 -2 2 3»Terbukti
4) f(x) jika dibagi (x²-4) memiliki sisa (x+3) . Jika dibagi x²+3x+2 memiliki hasil (x²-2x). Tentukan f(x) nya
Jawab : f(x) = (pembagi)(hasil) + sisa
F(x) = (x²+3x+2)(x²-2x) + x+3
F(x) = x⁴-2x³+3x³-6x²+2x²+x+3
F(x) = x⁴+x³-4x²-3x+3
Pembuktian=
Jika x⁴+x³-4x²-3x+3 dibagi x²-4 dengan pembagian bersusun pasti akan bersisa x+3 dengan hasl (x²+x)
Suku banyak f(x) jika dibagi (x²-4) sisanya x+3 . Dan jika dibagi x²+3x+2 hasilnya x²-2x. Maka f(x) nya adalah…
Jawab : (pembagi)(hasil)+sisa
(x²-4)(x²-2x)+ x+3 = x⁴-2x³-4x²-7x+3
JAWABAN
1) f(-2)=(-2)3-3(-2)+6
=-8+6+6
=4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 ⁺
1 -2 1 4 sisanya=4
2) f(x)=4×5+3×3+x+4 dibagi 2x+1
f(-1/2)= 4(-1/2)5+3(-1/2)3+(-1/2)+4
= -1/8-3/8-1/2+4
= -4/8-1/2=4
= -2/2+4
=3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisanya =3
3) (x-1)=3
(x-2)=4
Misal sisa: ax+b
F(1)= a+b=3 …….1
F(2)=2a+b=4 – …….2
a=1
substitusikan a=1 ke pers2
1+b=3
b=2
masukan a=1 & b=2 ke persamaan sisa
jadi sisanya adalah x+2
4) sisanya= (x+3) jika dibagi (x2-4) sedangkan saat dibagi x2+3x+2 memiliki hasil bagi (x2-2x), tentukan persamaan f(x)nya
Jawabannya:
F(x)= pembagi x hasil bagi + sisa
(x2+3x+2) (x2-2x) + x+3
(x+2) (x+1) x(x-2) +x+3
Jadi f(x)= (x2+3x+2) (x2-2x) +x+3
= x4-2×3+3×3-6×2+2×2-4x+x+3
=x4+x3-4×2-3x+3
5) f(x)= x4+3×3+x2-(P+x)+1
(x-2)=5
F(2)= (2)4+3(2)3+(2)2-(P+2)+1=35
16+24+4-P-2+1=35
-P+40+3=35
-P=35-43
P=8
jadi nilaiP=8
6) f(x)= x3+(ak+sa)x2+18a3
X+3a
Tentukan nilai k
Cara Horner
1 ak+2a 0 18a3
-3a -3a -3a2k+3a2 9a3k-9a3 +
1 ak-a -3a2k+3a2 9a3k+9a3
9a3k+9a3=0
9a3k=-9a3
k= -1
jadi nilai k =-1
7) f(x)= x3+4×2+11x+30
Tunjukan bahwa (x+5) merupakan faktornya
Jawabannya
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karna sisanya =0, maka x+5 merupakan faktor x3+4×2+11x+30
8) P(x)= 2×3-x2-7x+6
Tentukan faktor faktornya
Jawabannya
Jika semua koefisien ditambahlan dan hasilnya adalah 0 makan angka 1 merupakan akarnya
Cara horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah= (2×2+x-6) (x-1)
= (2x-3) (x+2) (x-1)
9) Dik (x-2) merupakan faktor dari P(x)= 2×3+x2+ax-6
Jawaban:
P(2)= 2(2)3+(2)2+2a-6
16+4+2a-6=0
14+2a=0
2a=-14
a=-7
substitusikan a=-7 ke persamaan P(x)= 2×3+x2+ax-6
2×3+x2+7x-6
(x-2) (2×2+5x+3)
(x-2) (2x+3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x+3) (x+1)
10) f(x)= x3-ax2+bx-2
(x-1)=>x=1 sisanya 0
(x+2)=>x=-2 sisanya -36
Tentukan a+b=…?
Jawaban
Cara Horner
1 -a b -2
1 1 -a+1 -a+1+b +
1 -a+1 -a+1+b 0
-2-a+1+b=0
-a+b=1 ……1
Cara Horner
1 -a b -2
2 -2 2a+4 -4a-8-2b +
1 -a-2 2a+4+b -36
-2-4a-8-2b=-36
-4a-2b=-26
:2
2a+b=13 ……2
-a+b=1 ……1
2a+b=13 -……2
-3a =-12 =>a=4
substitusikan a=4 ke persamaan1
4+b=1
b=5
jadi a+b
4+5=9
Sialahkan yang mahu menaggapi
Nomor 7 kan ada metode horner. Seharusnya 16 × -5 = -80 bukan -30. Dan bersisa -50 bukan 0
Suku banyak f(x) jika dibagi (x-1) sisanya 3
Jika dibagi (x-2) sisanya 4
Jika dibagi (x²-3x+2) maka sisanya?
Jawab :
Karena f(x) dibagi (x-1) maka f(1) = 3
Karena f(x) dibagi (x-2) maka f(-2) = 4
F(1) = 3 = a+b = 3
F(2) = 4 = 2a+b = 4
f(1) dan f(2) dieliminasi sehingga diperoleh
a= 1
hasil a subsitusikan ke persamaan
a+b=3
1+b=3
b=2
Maka sisa dari x²-3x+2
aX+B = x+2
Itu no3 Pa ipul
yupss
5. F(x) = x⁴+3x³+x²-(p+x)+1 dibagi (x-2) sisa 35. Maka p..?
Jawab :
Karena dibagi (x-2) maka f(2)
F(2) = 2⁴+3(2³)+2²-(p+2)+1 =35
= 16+24+4-(p+2)+1 =35
= 45-p-2 =35
= 43-p = 35
43-35=p
8=p
Ada yang mau tanggapi..?
Ada yang mahu naggapi..?
2. F(x) = 4X5+3X3+x+5 dibagi (2X+1) buktikan
Karena dibagi 2X+1 maka sisanya f(-1/2)
F(-1/2) = 4(-1/2)5+3(-1/2)3+(-1/2)+4
= 4(-1/32)+3(-1/8(-1/2)+4
= -1/8 + (-3/8) – 1/2 + 4
= -1/8 – 3/8 -4/8 + 32/8 = 24/8 = 3
Pembuktian dengan cara horner
X= -1/2
-1/2 | 4 0 3 0 1 4
| -2 1 -2 1 -1
———————+
4 -2 4 -2 2 3
TERBUKTI SISANYA 3
bagus
1. X³-3x+6 dibagi x+2, dengan teorema sisa,buktikan
Jawab : karena dibagi x+2 maka sisanya f(-2).
Subsitusikan dengan cara
= X³-3x+6
= (-2)³-3(-2)+6
= -8 – (-6) +6
= -8 +6+6
= 4
Pembuktiannya :
-2 | 1 -3 6
| -2 -10
————–+
1 -5 4
4 merupakan sisa pembagian. Dan terbukti .
Ada yang mau nanya..?
MUTIARA AZZAHRA
5611A3
Jawaban :
1) F(-2) = (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 +
1 -2 1 4 sisa = 4
2) F(x) = 4×5 +3×3 + X + 4 dibagi 2x + 1
F(-1/2) = 4(-1/2)5 + 3(-1/2)3 + (-1/2)+4
= -1/8 – 3/8 – ½ + 4
= -4/8 – ½ = 4
= -2/2 + 4
= 3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisa = 3
3) (X-1) = 3
(X-2) = 4
Misal sisa: ax + b
F(1) = a + b = 3 …….(1)
F(2) = 2a + b = 4 – ………(2)
a = 1
substitusikan a=1 ke persamaan 2
1+b=3
b=2
masukan a=1 dan b=2 ke persamaan sisa
Jadi sisanya adalah x + 2
4) Sisanya = (x + 3) jika dibagi (x2 – 4) sedangkan saat dibagi x2 + 3x + 2 memiliki hasil bagi (x2 – 2x), tentukan persamaan f(x)nya.
Penyelesaian:
F(x) = pembagi x hasil bagi + sisa
(x2 + 3x + 2) (x2 – 2x) + x+3
(x + 2) (x + 1) x(x-2) + X + 3
Jadi f(x) = (x2 + 3x + 2) (x2 – 2x) + x + 3
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x+x+3
= x4 + x3 – 4×2 – 3x+3
5) F(x) = x4 +3×3 +x2 – (P+x) + 1
(x-2)=5
Penyelesaian:
F(2) = (2)4 + 3(2)3 + (2)2 – (P+2) + 1 = 35
16 + 24 + 4-P-2+1=35
-P+40+3=35;
-P= 35 – 43
P = 8
Jadi nilai P = 8
6) X3 + (ak + 2a) x2 + 18a3 = (x + 3a)
= -3a3 + (ak + 2a) (-3a2) + 18a3 = -3a + 3a
= -27a3 + (ak +2a) 9a2 + 18a3 = 0
= -27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = -9a3
= k = -1
7) F(x) = x3 + 4×2 +11x+30
Tunjukan bahwa (x+5) merupakan faktornya.
Penyelesaian:
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karena sisanya = 0, maka x+5 merupakan faktor x3 +4×2 +11x+30
8) P(x) = 2×3 –x2 -7x+6
Tentukan faktor faktornya.
Penyelesaian:
Jika semua koefisien ditambahkan dan hasilnya adalah 0 maka angka 1 merupakan akarnya
Cara Horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah = (2×2 + x-6) (X-1)
= (2x-3) (x+2) (x-1)
9) Dik (x-2) merupakan faktor dari P(x)= 2×3 + x2 + ax-6
Penyelesaian:
P(2) = 2(2)3 + (2)2 + 2a – 6
16 + 4 + 2a – 6 = 0
14 + 2a = 0
2a = -14
a = -7
substitusikan a= -7 ke persamaan P(x) = 2×3 + x2 + ax – 6
2×3 + X2 + 7x – 6
(x-2) (2×2 + 5x + 3)
(x-2) (2x + 3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x + 3) (x+1)
10) F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x-2) bersisa -36, maka nilai a+b…
x-1 = 0
x = 1
Substitusikan :
F(1) = (1) – a (1) + b(1) – 2 = 0
1 – a + b – 1 = 0
-a + b – 1 = 0
-a + b = 1 …….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F(-2) = (-2)3 – a(-2)2 + b(-2) = -36
-8 – a4 – 2b – 2 = -36
-4a – 2b = -36 + 10
-4a – 2b = -26 …..pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b = 1 | x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1 = -4a – 2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a = 4
jadi, a+b = 4+5 = 9
bagus
No.3
Suku banyak f(x) jika dibagi (x-1) sisanya 3,jika dibagi (x-2) sisanya 4 jika f(x) dibagi dengan (x²+3x+2) maka tentukan sisanya
Jawaban…
Diketahui.
(x-1)=3
F(1)=3
(x-2)=4
F(2)=4
Ditanya sisanya ?
(x²-3x+2)=(x-1)
F(2)-f(1)x+2f(1)-1f(2)
2-12-1
S=(4-3)/1x+(2.3-1.4)/1
=x+(6-4)/1
=x+2
Dengan demikian sisanya adalah x+2.
Sekian dan terima kasih…
bagus, lanjut diskusi
No.2
Tentukan sisa pembagian f(x)=4x^5+3x³+x+4 dibagi (2x+1) buktikan…
Jawaban…
Diketahui : f(x)=4x^5+3x³+x+4 dibagi (2x+1)
Ditanya sisanya ?….
Pembahasan…
(2x+1)faktornya,berarti f(-1/2)=0
Kita subtitusikan ya guys
F(x) = 4x^5+3x³+x+4
F(-1/2)=4(-1/2)^5+3(-1/2)³+ (-1/2)+4
=-1/8-3/8-1/2+4
=-4/8-1/2=4
=-2/2+4
=3
Dengan demikian sisanya adalah 3.
Lalu mari kita buktikan dengan cara pembagian secara horner…
2x+1 | 4 0 3 0 1 4
X:-1/2| -2 1-2 1-1 +
4-2 4-2 2[3]-> sisanya adalah 3 Terbukti
Sekian dan Terima Kasih
Pertanyaan
1.X³-3x+6 dibagi (x+2) dengan teorema sis buktikan.
Jawaban…
Diketahui:P(x):x³-3x+6
Dibagi (X+2)
Ditanya : sisa (x)
Pembahasan…
Pertama-tama kita harus mendapatkan nilai ‘x’ nya terlebih dahulu…
(x+2)
x+2=0
x=-2
Setelah itu,kita subtitusikan kedalam
Rumus yang disediakan…
P(x)=x³-3x+6
=(-2)³-3(-2)+6
=-8+6+6
=4
Dengan demikian kita mendapat nilai 4.
Dengan demikian,kita bisa membuktikan dengan menggunakan cara horner sebagai berikut…
x+2 | 1 0 3 6
x:-2| -2 4-2 +
1-2 1[4] -> sisanya adalah 4
Sekian dan Terima kasih
Saya mau nanya ini yang dimaksud dengan “X³-3X+6=(X+2)(h(x)+s(x)”
Saya mengerti kalau x+2 sebagai pembagi lalu diubah menjadi f(-2) lalu “h(x)” ini jadi apa dijelaskan sesuai dengan rumus yang diberikan teman kita diatas secara sistematis dan mengapa ini berbeda sangat dengan rumus yang diatas contohnya!
Oh,jadi h(x) itu sebagai hasil bagi lalu ditambah s(x)sisa bagi ya
bagus, silahkan yang lain menanggapi
kepada teman² yang baik itu jawaban teman kita kayak gini maksudnya gimana sih
X³-3X+6=(X+2)(h(x)+s(x)
tolong dijelaskan diatas lalu itu yang dimaksud dengan ini apa ya? (x+2)(h(x)+s(x)
buat apa?
x+2 sebagai pembagi jadi f(-2) lalu pertanyaan saya selanjutnya adalah h(x) ini apa artinya ini saya tidak diketahui apa tidak ? atau jadi ditanya h(x) tersebut tolong dipermudah ?
Silahkanuntuk yang lainnya mendiskusikan
Penyelesaian:
1)Dik:x^3-3x+6 dibagi (x+2)
Dit:teorema sisa dan buktikan
Jwb:
Teorema sisa»f(x) dibagi (x+a) maka sisanya f(-a).Jadi;
F(-a)=x^3-3x+6
F(-2)=(-2)^3-3(-2)+6
=-8+6+6
=-8+12
=4
Buktinya:
»Menggunakan Metode Horner
-2|1 0 -3 6
-2 4 -2
_____________+
1-2 1 4»»sisanya=4(terbukti)
Bagus, ada yang berpendapat lain..?
1.f(-2)=(-2)3-3(-2)+6
=-8+6+6
=4
Pembuktian
Cara Horner
1 0 -3 6
-2 -2 1 4 sisanya=4
2.f(-½)=4(-½)5+3(-½)3+(-½)+4
=-⅛-⅜-½+4
=-2/2+4
=3
Pembuktian
Cara Horner
4 0 3 0 14
-½ -2 1 -2 2 3 sisanya:3
3.(x-1)=3
(x-2)=4
misal sisa ax+b
f(1)=a+b=3…..1
f(2)=2a+b=4…..2
a:1
subsitusikan a=1 ke pers 1
1+b=3
b=2
masukkan a=1&b=2 kepers sisa jadi sisanya adalah x+2
4.f(x)=pembagi x hasil bagi +sisa
(x2+3x+2)(x2-2x)+x+3
jadi f(x)=(x2+3x+2)(x2-2x)+x+3
x4-2×3+3×3-6×2+2×2-4x+x+3
x4+x3-4×2-3x+3
5.f(2)=(2)4+3(2)3+(2)2-(p+2)+1=35
16+24+4-p-2+1=35
-p+40+3=35
-p=35-43
p=8
6.Cara Horner
1 ak+2a 0 1 8a 3
-3a -3a -3a2k+3a2 9a3k-9a3+1ak-a-3a2k+3a2 9a3k+9a3
9a3k+9a3=0
9a3k=-9a3k
k=-1
7.Cara Horner
1 4 1 1 3 0
-5-55-30(+)
1-1160
karena sisa 0 makax+5 merupakan faktor x3+4×2+11+30
8.Cara Horner
2 -1 -7 6
1 2 1 -6
2 1 -6 0
jadi faktornya adalah
(2×2+x-6)(x-1)=(2x-3)(x+2)(x-1)
9.P(2)=2(2)3+(2)2+2a-6
=16+4+2a-6=0
=14+2a=0
=a=-7
subsitusikan a=-7 ke pers p(x)=2x+3+x2+ax-6
(x-2)(2×2+5x+3)
(x-2)(2x+3)(x+1)
jadi faktor lainnya(x-2)(2x+3)(x+1)
10.f(x)=x3-ax2+bx-2
(x-1)=>>x=1 sisanya 0
(x+2)=>>x=-2 sisanya -36
jawab dengan cara horner
1 -a b -2
1 1 -a + 1-a + 1 + b
1-a+1-a+1+b 0
1-a+1-a+1+b =0
-2-a+1+b=0
-a+b=1……1
1-a b-2
2-2 2a+4 -4a-8 -2b
1-a-2 2a+4 +b-36
-2-4a-8-2b=-36
-4a-2b=-26….2
subsitusikan a=4 ke pers 1
2a+b=13….2
-4+b=1 .b=5
-a+b=1….1
2a+b=13…..2 jadi a+b -3a=-12,a=4
a+b ==>4+5=9
Ada yang punya cara lain..?
Dermawan,saya ingin bertanya
Itu kok nomer 6 tiba-tiba langsung -3a²k+3a²+ 9a³k+9a³
Saya hitungnya kok depan nya masih ada ak-3 nya lagi.. bisa jelaskan??
Sialahkan dilanjutkan
Ada yang mau menaggapi..?
1.tentukan teorema sisa X3-3X+6 dibagi dengan (x+2). buktikan!
penyelesaian :
x+2=0
x=-2
F(x)=X3-3X+6
F(-2)=(-2)3-3(-2)=6
=-8+6+6=4
Dibuktikan dgn cara horner pembagi -2 dibagi dengan 1 0 -3 6 -2 4 -2+
Hasilnya 1 -2 1 4 dan 4 itu sisa
2.tentukan sisa pembagian F(X)=4X5+3X3+X+4 Dibagi(2X-1).buktikan!
Penyelesaian :
2X+1=0
2X=-1
X=-1/2
F(X)=4X5+3X3+X+4
F(-1/2)=4(-1/2)5+3(-1/2)3+(-1/2)+4
=-1/8+(-3/8)+7/2
=-4/8+7/2
=3
Dibuktikan dengan cara horner 4 0 3 0 1 4
-1/2 -2 1 -2 1 -1+
Hasilnya 4 -2 4 -2 2 3 dan sisanya 3
3.suku banyak F(X)jika dibagi (X-1)Sisanya 3, jika dibagi (x-2)sisanya 4, jika F(x) dibagi dengan (X2-3X+2)maka tentukan sisanya.
Penyelesaian:
(X-1)=3
(X-2)=4
F(1)=a+b=3
F(2)=2a+b=4
a=1
1+b=3
b=2
jadi,aX+b=X+2
4.suku banyak F(X)memiliki sisa (X+3)jika dibagi (X2-4).sedang saat dibagi (X2+3X+2) memiliki hasil bagi(X2-2X)tentukan persamaan F(X) nya.
Penyelesaian:
F(X)= pembagi X hasil bagi + sisa
(X2+3X+2) (X2-2X)+ X+3
(X+2)(X+1) X (X-2) + X+3
F(X)=(X2+3X+2)(X2-2X) + X+3
=X4-2X3+3X3-6X2+2X2-4X+X+3
=X4+X3-4X2-3X+3
5.suku banyak F(X)=X4+3X+X2-(P+X)+1 dibagi dengan X-2 memberikan sisa =35. tentukan nilai P
Penyelesaian:
F(X)=X4+3X3+X2-(P+X)+1
(X-2)=5
F(2)=(2)4+3(2)3+(2)2-(P+2)+1=35
=16+24+4-P-2+1=35
=-P+40+3=35
=-P=35-43
=-P=-8
P=8
6.tentukan nilai K sehingga (X+3a) merupakan faktor dari X3+(ak+2a)X2+18a3
Penyelesaian:
X3+(ak+2a)x 2+18a3=(X+3a)
=-3a3+(ak+2a)(-3a2)+18a3=-3a+3a
=-27a3+(ak+2a)9a2+18a3=0
=-27a3+9a3k+18a3+18a3=0
=9a3+9a3k=0
=9a3k=-9a3
k=-1
7.tunjukan bahwa (X+5) adalah faktor dari X3+4X2+11x+30
Penyelesaian:
F(X)=X3+4X2+11X+30
Cara horner
1 4 11 30
-5 -5 5 -30+
hasilnya 1 -1 16 0 karena sisanya 0 maka X+5 merupakan faktor dari X3+4X+11X+30
8.tentukan faktor faktor dari P(X)=2X3-X2-7X+6
Penyelesaian:
jika semua koefisien ditambahkan dan hasilnya 0, maka angka 1 merupakan akar nya
cara horner
2 -1 -7 6
1 2 1 -6+
2 1 -6 0 jadi faktor faktor nya adalah (2X2+X-6)(X-1)=(2X-3)(X+2)(X-1)
9.Diketahui(X-2) adalah faktor, P(X)=2X3+X2+aX-6,tentukan faktor faktor lain nya
Penyeleaian:
P(-2)=2(2)3+(2)2+2a-6
=16+4+2a-6=0
=14+2a=0
=2a=-14
a=-7
substitusikan a=-7 ke persamaan P(X)=2X3+X2+aX-6
=2X3+X2+7x-6
=(X-2)(2X2+5x+3)
=(X-2)(2X+3)(X+1)
jadi faktor lain nya adalah (X-2)(2X+3)(X+1)
10.Suku banyak F(X)=X3-aX2+bX-2 mempunyai faktor (X-1).jika di bagi oleh (X+2) bersisa -36, maka nilai a+b adalah
Penyelesaian:
cara horner
1 -a b -2
1 1 -a+1 -a+1+b+
1 -a+1 -a+1+b 0
-2-a+1+b=0
-a+b=1…….1
cara horner
1 -a b -2
2 -2 2a+4 -4a-8-2b+
1 -a-2 2a+4+b -36
-2-4a-8-2b=-36
-4a-2b=-26
dibagi 2 = 2a+b=13
-a+b=1……..1
2a+b=13…….2
-3a=-12
a=4
substitusikan a=4 ke persamaan 1
=4+b=1
b=5 jadi a+b=4+5=9
Lengkap,…ada yang mau menanggapi..?
1)(X+2) faktornya brarti, f(-2)=0
f(-2)=x3-3x+6
= -2.3-3.-2+6
= -8+6+6
=-8+12
= 4
PEMBUKTIAN menggunakan cara horner
-2 1 -3 6
-2 2
1 -1 4=>sisa
Jadi sisa nya 4
2) (2x +1) faktornya brarti, f(-1/2)
f(-1/2) = 4×5+3×3+x+4
= 4(-1/2)5+3(-1/2)3-1/2+4
=4(-1/32)+3(-1/8)-1/2+4
=-1/8-3/8-1/2+4
=-4/8-1/2+4
=-1/2-1/2+4
=-1+4
=3
PEMBUKTIAN dengan cara horner
-1/2 4 0 3 0 1 4
-2 1 -2 1 1
4 -2 4 -2 2 3=> sisa
Jadi sisa nya 3
5) (X-2)=> x=2
f(x) = x4+3×3+x2-(p+x)+1
f(2) = 24+3.23+22-(p+2)+1=35
= 16+24+4-(p+2)+1=35
16+24+4-p-2=35-1
16+24+4-p-2=34
-p=34-16-24-4+2
-p=-8
p=8
7) Cara bersusun
X+5 x3+4x+11x+30
x3+5x
-x2+11x+30
-x2+5x
6x+30
6x +30
0=> sisa
Kalo sisanya 0 berarti terbukti
kalo faktornya ada(x-2)
9) Diketahui (x-2) adalah faktor , P(x) 2×3+x2+ax-6
faktor lainnya
X=2
P(x)= 2×3+x2+ax-6
P(2)=2.23+22+a2-6=0
16+4+2a-6=0
14+2a=0
2a=-14
a= -7
Persamaan nya: 2×3+x2+7x-6
Faktor dari :2×3+x2+7x-6
=(X-2) (2×2+5x+3)
= (X-2) (2×2+5x+3)
=(x-2) (2x+3) (x+1)
Jadi,faktor lain dari persamaan tersebut adalah
(2x+3) (x+1)
1) P(-2)=(-2)3-3(-2)+6
=(-8)-(-6)+6
=4
Pembuktian
-2 1 0 -3 6
-2 4 -2
1 -2 1 4 terbukti
2) f(-1/2)= 4(-1/2)5+3(-1/2)3+(-1/2)+4
= (-1/8) – 3/8 – 1/2 +4
= (-4/8) – 1/2 +4
= -1 + 4
= 3
Pembuktian:
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1
4 -2 4 -2 2 3
7) cara horner
-5 1 4 11 30
-5 5 -30
1 -1 6 0
Karena sisa pembagiannya 0 maka (x-5) merupakan faktor dari x3+4×2+11x+30
8) P(x)= 2×3-x2-7x+6
(x+2) (2x-3) (x+1)
Jadi, faktor-faktor dari P(x)= 2×3-x2-7x+6 adalah (x+2) (2x-3) (x+1)
Pembahasan
1. F(-2) = 1. (-2)3 – 3 (-2) + 6
= -8 + 6 + 6
= 4
Pembuktian
Menggunakan metode horner
-2 1 0 -3 6
-2 4 -2
1 -2 1 4 sisa pembagian
Terbukti
2. 2x + 1 = 0
2x = -1
X = -1/2
P(-1/2) = 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 4(-1/32) + 3(-1/8) + (-1/2) + 4
=-1/8 + (-3/8) + (-1/2) +4
=-1/8 + (-3)/8 +(-4)/8 +32/8
= 24/8 = 3
Pembuktian
Menggunakan metode horner
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1
4 -2 4 -2 2 3 sisa pembagian = 3 ( terbukti )
8. Faktor dari 2x – x2 – 7x + 6
Metode horner
Misal dibagi 1 2 -1 -7 6
2 1 -6
2 1 -6 0
jadi 2×2 + × -6 = 0
( 2x – 3 ) ( x + 2 )
2x – 3 = 0 x = -2
2x = 3
X = 3/2
Jadi 2×3 – x – 7x + 6 mempunyai faktor :
(X- 1) ,( x – 3/2 ) ,( x + 2 )
1. x3-3x+6=(x+2)(h(x))+s(x)
Ditanya: s(x)
Penyelesaian
Subtitusikan X=-2
f(-2)=(-2)3-3(-2)+6
f(-2)=4
Metode Horner
-2 1 0 -3 6
-2 4 -2
1 -2 1 4
Jadi terbukti sisanya adalah 4
2. 4×5+3×3+x+4=(2x+1)(h(x))+s(x)
Ditanya : s(x)
Penyelesaian
Subtitusikan X=-1/2
f(-1/2)=4(-1/2)5+3(-1/2)3+(-1/2)+4
f(-1/2)=3
Metode Horner
-1/2 4 0 3 0 1 4
-2 1 -2 1 1
4 -2 4 -2 2 3
Jadi terbukti sisanya adalah 3
3. f(x)=(x-1)(h(x))+3
f(x)=(x-2)(h(x))+4
f(x)=[(x-2)(x-1)](h(x))+s(x)
Ditanyas(x)
Penyelesaian
Misal s(x) adalahax+b, subtitusikan X=1 dan X=2 pada fungsi f(x)=[(x-2)(x-1)](h(x))+s(x)
f(1)=3
3=a+b
f(2)=4
4=2a+b
Eleminasikan (a+b=3) dengan (2a+b=4)
Hasilnya yaitu a=1 &b=2
Subtitusikan a dan b ke s(x)
Makas isanya yaitu s(x)=x+2
4. f(x)=(x2-2)(h(x))+(x+3)
f(x)=(x2+3x+2)(x2-2x)+(ax+b)
Ditanya f(x)
Penyelesaian
Subtitusikan X=2 dan X=-2 (dari akarakar (x2-2)) ke f(x)=(x2+3x+2)(x2-2x)+(ax+b)dan f(x)=(x2-2)(h(x))+(x+3)
f(2)=5
5=2a+b
f(-2)=1
1=-2a+b
Eleminasi (2a+b=5) dan (-2a+b=1). Hasilnya a=1 dan b=3
Jadi, f(x)=(x2+3x+2)(x2-2x)+(x+3)
f(x)=x4+x3-4×2-3x+3
5. x4+3×3+x2-(P+x)+1=(x-2)(h(x))+35
Ditanya P=
Penyelesaian
Subtitusikan X=2 ke persamaan x4+3×3+x2-(p+x)+1=(x-2)(h(x))+35
f(2)=35
35=43-P
P=8
Jadi nilai P adalah 8
6. Nilai K jika (x+3a) adalahf aktor dari x3+(aK+2a)x2+18a3
Penyelesaian
jika (x+3a) adalahf aktor dari x3+(aK+2a)x2+18a3
maka f(-3a)=0
subtitusikan X=-3a
f(-3a)=9a3+9Ka3
9a3+9Ka3=0
Maka nilai a yang memenuhi adalah 1
7. (x+5) adalahfaktordari x3+4×2+11x+30
Penyelesaian
Jika(x+5) adalah faktor dari x3+4×2+11x+30
Makaf(-5)=0
Subtitusikan X=-5 kex3+4×2+11x+30
(-5)3+4(-5)2+11(-5)+30=0
0=0 terbukti
Dengan metodehornerpun akan menghasilkan sisa 0 yang berarti (x+5) adalah factor darix3+4×2+11x+30
8. Faktordari P(x)=2×3-x2-7x+6
Penyelesaian
Gunakan metode horner
Gunakan 1 sebagaicalonakar
1 2 -1 -7 6
2 1 -6
2 1 -6 0
Jadi 1atau (x-1)adalahfaktordari P(x)
2×2+x-6=0
(x+2)(2x-3)=0
Jadi faktor faktor P(x) adalah (x-1)(x+2)(2x-3) atau 1, -2, 3/2
9. (x-2) adalah faktor P(x)=2×3+x2+ax-6
Tentukan faktor yang lain
Penyelesaian
P(2)=0
Subtitusikan X=2
2a+14=0
a=-7
P(x)=2×3+x2-7x-6
Metode horner
2 2 1 -7 -6
4 10 6
2 5 3 0
2×2+5x+3=0
(x+1)(2x+3)=0
Jadi faktornya yaitu(x+1),(2x+3),(x-2) atau -1, 2, -3/2
10. (x-1) faktordari f(x)=x3-ax2+bx-2
x3-ax2+bx-2=(x+2)(h(x))-36
tentukannilai a+b
penyelesaian
(x-1) faktordari f(x)=x3-ax2+bx-2
Makaf(1)=0
1-a+b-2=0
b-a=1
subtitusikan X=-2 (faktordari x+2) ke persamaan f(x)
f(-2)=-36
-8-4a-2b-2=-36
-2a-b=-13
Subtitusikan b-a=1 dengan -2a-b=-13
Maka a=4 dan b=5
Nilai a+b=4+5=9
Jadi a+b=9
JENIEKAFITRIANI
XI MIA 1
Bagi yang belum hadir Silahkan menangggapi…
1. x3-3x+6=(x+2)(h(x))+s(x)
Ditanya: s(x)
Penyelesaian
Subtitusikan X=-2
f(-2)=(-2)3-3(-2)+6
f(-2)=4
Metode Horner
-2 1 0 -3 6
-2 4 -2
1 -2 1 4
Jadi terbukti sisanya adalah 4
2. 4×5+3×3+x+4=(2x+1)(h(x))+s(x)
Ditanya : s(x)
Penyelesaian
Subtitusikan X=-1/2
f(-1/2)=4(-1/2)5+3(-1/2)3+(-1/2)+4
f(-1/2)=3
Metode Horner
-1/2 4 0 3 0 1 4
-2 1 -2 1 1
4 -2 4 -2 2 3
Jadi terbuktisisany aadalah 3
3. f(x)=(x-1)(h(x))+3
f(x)=(x-2)(h(x))+4
f(x)=[(x-2)(x-1)](h(x))+s(x)
Ditanyas(x)
Penyelesaian
Misal s(x) adalahax+b, subtitusikan X=1 dan X=2 pada fungsi f(x)=[(x-2)(x-1)](h(x))+s(x)
f(1)=3
3=a+b
f(2)=4
4=2a+b
Eleminasikan (a+b=3) dengan (2a+b=4)
Hasilnya yaitu a=1 &b=2
Subtitusikan a dan b ke s(x)
Maka sisanya yaitu s(x)=x+2
4. f(x)=(x2-2)(h(x))+(x+3)
f(x)=(x2+3x+2)(x2-2x)+(ax+b)
Ditanya f(x)
Penyelesaian
Subtitusikan X=2 dan X=-2 (dari akar akar (x2-2)) ke f(x)=(x2+3x+2)(x2-2x)+(ax+b)danf(x)=(x2-2)(h(x))+(x+3)
f(2)=5
5=2a+b
f(-2)=1
1=-2a+b
Eleminasi (2a+b=5) dan (-2a+b=1). Hasilnya a=1 dan b=3
Jadi, f(x)=(x2+3x+2)(x2-2x)+(x+3)
f(x)=x4+x3-4×2-3x+3
5. x4+3×3+x2-(P+x)+1=(x-2)(h(x))+35
Ditanya P=
Penyelesaian
Subtitusikan X=2 kepersamaanx4+3×3+x2-(p+x)+1=(x-2)(h(x))+35
f(2)=35
35=43-P
P=8
Jadi nilai P adalah 8
6. Nilai K jika (x+3a) adalah faktordari x3+(aK+2a)x2+18a3
Penyelesaian
jika (x+3a) adalahfaktordari x3+(aK+2a)x2+18a3
maka f(-3a)=0
subtitusikan X=-3a
f(-3a)=9a3+9Ka3
9a3+9Ka3=0
Maka nilai a yang memenuhiadalah 1
7. (x+5) adalahfaktordari x3+4×2+11x+30
Penyelesaian
Jika(x+5) adalah faktordari x3+4×2+11x+30
Makaf(-5)=0
Subtitusikan X=-5 kex3+4×2+11x+30
(-5)3+4(-5)2+11(-5)+30=0
0=0 terbukti
Dengan metodehornerpun akanmenghasilkan sisa 0 yang berarti (x+5) adalah factor darix3+4×2+11x+30
8. Faktordari P(x)=2×3-x2-7x+6
Penyelesaian
Gunakanmetodehorner
Gunakan 1 sebagai calonakar
1 2 -1 -7 6
2 1 -6
2 1 -6 0
Jadi 1atau (x-1)adalahfaktordari P(x)
2×2+x-6=0
(x+2)(2x-3)=0
Jadifaktorfaktor P(x) adalah (x-1)(x+2)(2x-3) atau 1, -2, 3/2
9. (x-2) adalahfaktor P(x)=2×3+x2+ax-6
Tentukanfaktor yang lain
Penyelesaian
P(2)=0
Subtitusikan X=2
2a+14=0
a=-7
P(x)=2×3+x2-7x-6
Metode horner
2 2 1 -7 -6
4 10 6
2 5 3 0
2×2+5x+3=0
(x+1)(2x+3)=0
Jadi faktornya yaitu(x+1),(2x+3),(x-2) atau -1, 2, -3/2
10. (x-1) faktordari f(x)=x3-ax2+bx-2
x3-ax2+bx-2=(x+2)(h(x))-36
tentukannilai a+b
penyelesaian
(x-1) faktordari f(x)=x3-ax2+bx-2
Makaf(1)=0
1-a+b-2=0
b-a=1
subtitusikan X=-2 (faktordarix+2) kepersamaan f(x)
f(-2)=-36
-8-4a-2b-2=-36
-2a-b=-13
Subtitusikanb-a=1dengan-2a-b=-13
Maka a=4 dan b=5
Nilai a+b=4+5=9
Jadi a+b=9
JENIEKAFITRIANI5611A1
Jawaban ok..tapi namanya JENIEKAFITRIANI5611A1, lain kali jangan disambung jadi JENI EKA FITRIANI 5611A1 lebih mudah mencarinya
oke pak,, salahnya dimana ya pak? mohon bimbingannya…
Silahkan, teman-temanya mendiskusikan terlebih dahulu…dengan memberikan komen JENIEKAFITRIANI5611A1(pakai spasi kali JENI EKA FITRIANI 5611A1)
2). Tunjukkan bahwa (x+5) adalah faktor dari x3+4×2+11x+30.
Penyelesaian:
x+5=0
x=-5
p(x)=x3+4×2+11x+30
p(-5)=(-5)3+4(-5)2+11(-5)+30
=-125+100-55+30
=-50
Pembuktian dengan cara horner
1 4 11 30
-5 -5 5 -80 +
1 -1 16 -50 sisanya=-50
Karena sisanya -50,maka (x+5) bukan faktor dari x3+4×2+11x+30
9). Diketahui (x-2) adalah faktor p(x)=2×3+x2+ax-6,tentukan faktor lainnya.
Penyelesaian:
p(x)=2×3+x2+ax-6
p(2)=2(2)3+(2)2+2a-6=0
16+4+2a-6=0
14+2a=0
2a=-14
a=-7
P(x)=2×3+x2-7x-6 berarti koefisien p(x) adalah 2 1 -7 -6
Pembagian horner:
2 1 -7 -6
2 4 10 6 +
2 5 3 0
Hasil baginya adalah 2×2+5x+3=(2x+3)(x+1)
Jadi,faktor yang lainnya adalah (2x+3)(x+1)
10). Suku banyak f(x)=x3-ax2+bx-2 mempunyai faktor (x-1). Jika dibagi oleh (x+2) bersisa -36,maka nilai a+b adalah…
Penyelesaian:
Suku banyak f(x)=x3-ax2+bx-2
(x-1) faktor f(x)-> f(1)=0
f(1)=1-a+b-2=0
-a+b=1…(1)
Dibagi (x+2) bersisa -36,f(-2)=-36
f(-2)=(-2)3-a(-2)2+b(-2)-2=-36
-8-4a-2b-2=-36
-4a-2b=-36+10
-4a-2b=-26
2a+b=13…(2)
Eliminasi persamaan (1) dan (2)
-a+b=1
2a+b=13 –
-3a=-12
a=4
Substitusikan a=4 ke persamaan (2)
-a+b=1
-4+b=1
b=5
Jadi,nilai a+b=4+5=9
1.) X3 – 3x +6 =X+2X + 2 = 0X = -2Substitusikan :X3 – 3x + 6= (-2)3 – 3(-2) + 6= -8 + 6 + 6= 4Pembuktian, menggunakan aturan horner :-2 1 0 -3 6-2 4 -2 (+)1 -2 1 4Terbukti bahwa sisanya adalah 42.) 4×5 + 3×3 + x + 4 =2x + 12x + 1 = 02x = -1X= -1/2Substitusikan :4×5 + 3×3 + x + 4= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4= 3Pembuktian, menggunakan aturan horner :-1/2 4 0 3 0 1 4-2 1 -2 1 -1 (+)4 -2 4 -2 2 3Terbukti bahwa sisanya adalah 33.) ( x – 1 ) = 3f( 1 ) = 3( x – 2 ) = 4f( 2 ) = 4( x2 – 3x + 2 ) = ( x – 1 )f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )2 – 1 2 – 1s= (4-3)/1 x+(2 .3-1 .4)/1S=x+(6-4)/1S=x+24.) f( x ) = pembagi x hasil bagi + sisa= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x + x + 3= x4 + x3 – 4×2 – 4x + x + 3= x4 + x3 – 4×2 – 3x + 35.) f( 2 ) = 35= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35= 16 + 24 + 4 – p – 2 + 1 = 35= 43 – p = 35– p = 35 – 43– p = -8p = 86.) x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )– 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a– 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0– 27a3 + 9a3k + 18a3 + 18a3 = 09a3 + 9a3k = 09a3k = – 9a3k = -17.)cara susunx + 5 x3 + 4×2 + 11x + 30×3 + 5×2 –-x2 + 11x +30-x2 + 5x –6x + 306x + 30 –0 => sisa8.) 2×3 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)Jadi , faktor-faktor dari 2×3 – x2 – 7x + 6 adalah( x + 2)(2x – 3)(x + 1)9.) P(x) = 2×3 + x2 +ax – 6P(2) = 2(2)3 + 22 +a(2) – 6= 16 + 4 + 2a – 6 = 02a = -14a = -7persamaannya : 2×3 + x2 + 7x – 6faktor dari 2×3 + x2 + 7x – 6= ( x – 2 )(2×2 + 5x + 3 )= ( x – 2 )( 2x + 3 )( x + 1 )Jadi , faktor lain dari persamaan di atas adalah( 2x + 3 )( x + 1)10.) F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….x – 1 = 0x = 1substitusikan :f (1) = (1) – a (1) + b (1) – 2 = 01 – a + b – 2 = 0-a + b – 1 = 0-a + b = 1……….pers (1)X + 2 = 0X = -2Substitusikan :F (-2) = (-2)3 – a(-2)2 + b (-2) = -36-8 – a4 – 2b – 2 = – 36-4a – 2b = -36 + 10-4a – 2b = -26……….pers (2)Eliminasi persamaan 1 dan 2 :-a + b =1 |x 4 = -4a + 4b = 4-4a – 2b = -26 |x 1= -4a -2b = -26 –6b = 30b = 5-a + b = 1-a + 5 = 1-a = -4a= 4
Dimas saputra XI MIA 3
Cuma nulis nama saja,…dibaca kerjaan temanmu salah apa tidak…?, kode
JAWABAN
1) f(-2)=(-2)3 -3(-2)+6
=-8+6+6
=4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 ⁺
1 -2 1 4 sisanya=4
2) f(x)=4×5+3×3+x+4 dibagi 2x+1
f(-1/2)= 4(-1/2)5 +3(-1/2)3 +(-1/2)+4
= -1/8-3/8-1/2+4
= -4/8-1/2=4
= -2/2+4
=3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisanya =3
3) (x-1)=3
(x-2)=4
Misal sisa: ax+b
F(1)= a+b=3 …….1
F(2)=2a+b=4 – …….2
a=1
substitusikan a=1 ke pers2
1+b=3
b=2
masukan a=1 & b=2 ke persamaan sisa
jadi sisanya adalah x+2
4) sisanya= (x+3) jika dibagi (x2-4) sedangkan saat dibagi x2 +3x+2 memiliki hasil bagi (x2 -2x), tentukan persamaan f(x)nya
Jawabannya:
F(x)= pembagi x hasil bagi + sisa
(x2 +3x+2) (x2 -2x) + x+3
(x+2) (x+1) x(x-2) +x+3
Jadi f(x)= (x2 +3x+2) (x2 -2x) +x+3
= x4 -2×3 +3×3 -6×2 +2×2 -4x+x+3
= x4 +x3 -4×2 -3x+3
5) f(x)= x4 +3×3 +x2 -(P+x)+1
(x-2)=5
F(2)= (2)4 +3(2)3 +(2)2 -(P+2)+1=35
16+24+4-P-2+1=35
-P+40+3=35
-P=35-43
P=8
jadi nilai P=8
6) f(x)= x3 +(ak+sa)x2 +18a3
X+3a
Tentukan nilai k
Cara Horner
1 ak+2a 0 18a3
-3a -3a -3a2 k+3a2 9a3 k-9a3 +
1 ak-a -3a2 k+3a2 9a3 k+9a3
9a3 k+9a3=0
9a3 k=-9a3
k= -1
jadi nilai k =-1
7) f(x)= x3 +4×2 +11x+30
Tunjukan bahwa (x+5) merupakan faktornya
Jawabannya
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karna sisanya =0, maka x+5 merupakan faktor x3 +4×2 +11x+30
8) P(x)= 2×3 -x2 -7x+6
Tentukan faktor faktornya
Jawabannya
Jika semua koefisien ditambahlan dan hasilnya adalah 0 makan angka 1 merupakan akarnya
Cara horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah= (2×2 +x-6) (x-1)
= (2x-3) (x+2) (x-1)
9) Dik (x-2) merupakan faktor dari P(x)= 2×3 +x2 +ax-6
Jawaban:
P(2)= 2(2)3 +(2)2 +2a-6
16+4+2a-6=0
14+2a=0
2a=-14
a=-7
substitusikan a=-7 ke persamaan P(x)= 2×3 +x2 +ax-6
2×3 +x2 +7x-6
(x-2) (2×2 +5x+3)
(x-2) (2x+3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x+3) (x+1)
10) f(x)= x3-ax2+bx-2
(x-1)=> x=1 sisanya 0
(x+2)=> x=-2 sisanya -36
Tentukan a+b=…?
Jawaban
Cara Horner
1 -a b -2
1 1 -a+1 -a+1+b +
1 -a+1 -a+1+b 0
-2-a+1+b=0
-a+b=1 ……1
Cara Horner
1 -a b -2
2 -2 2a+4 -4a-8-2b +
1 -a-2 2a+4+b -36
-2-4a-8-2b=-36
-4a-2b=-26
:2
2a+b=13 ……2
-a+b=1 ……1
2a+b=13 – ……2
-3a =-12 => a=4
substitusikan a=4 ke persamaan1
4+b=1
b=5
jadi a+b
4+5=9
Tiefanny amilya lauretta marbun 10 mipa 3
Jawaban
1.) X3 – 3x +6 =
X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2.) 4×5 + 3×3 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
4×5 + 3×3 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3.) ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 – 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4.) f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x + x + 3
= x4 + x3 – 4×2 – 4x + x + 3
= x4 + x3 – 4×2 – 3x + 3
5.) f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
– p = 35 – 43
– p = -8
p = 8
6.) x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
– 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
– 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
– 27a3 + 9a3k + 18a3 + 18a3 = 0
9a3 + 9a3k = 0
9a3k = – 9a3
k = -1
7.)cara susun
x + 5 x3 + 4×2 + 11x + 30
x3 + 5×2 –
-x2 + 11x +30
-x2 + 5x –
6x + 30
6x + 30 –
0 => sisa
8.) 2×3 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 2×3 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9.) P(x) = 2×3 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 2×3 + x2 + 7x – 6
faktor dari 2×3 + x2 + 7x – 6
= ( x – 2 )(2×2 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10.) F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = – 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
Buat kode kelasnya tolong diperhatikan biar tdk tertukar dengan kelas lain
1). X3 – 3x +6 = X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2). 45 + 33 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
45 + 33 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3). ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4). f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 23 + 33 – 62 + 22 – 4x + x + 3
= x4 + x3 – 42 – 4x + x + 3
= x4 + x3 – 42 – 3x + 3
5). f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
= p = 35 – 43
= p = -8
= p = 8
6). x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
= 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
= 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
= 27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = 9a3
= k = -1
7). cara susun
x + 5 x3 + 42 + 11x + 30
x3 + 52
-x2 + 11x +30
-x2 + 5x
6x + 30
6x + 30
0=sisa
8). 23 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 23 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9). P(x) = 23 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 23 + x2 + 7x – 6
faktor dari 23 + x2 + 7x – 6
= ( x – 2 )(22 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10). F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
Jawaban
1.) X3 – 3x +6 =
X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2.) 4×5 + 3×3 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
4×5 + 3×3 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3.) ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 – 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4.) f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x + x + 3
= x4 + x3 – 4×2 – 4x + x + 3
= x4 + x3 – 4×2 – 3x + 3
5.) f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
– p = 35 – 43
– p = -8
p = 8
6.) x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
– 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
– 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
– 27a3 + 9a3k + 18a3 + 18a3 = 0
9a3 + 9a3k = 0
9a3k = – 9a3
k = -1
7.)cara susun
x + 5 x3 + 4×2 + 11x + 30
x3 + 5×2 –
-x2 + 11x +30
-x2 + 5x –
6x + 30
6x + 30 –
0 => sisa
8.) 2×3 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 2×3 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9.) P(x) = 2×3 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 2×3 + x2 + 7x – 6
faktor dari 2×3 + x2 + 7x – 6
= ( x – 2 )(2×2 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10.) F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = – 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
Kode kelas belum terisi
Jawaban
1.) X3 – 3x +6 =
X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2.) 4×5 + 3×3 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
4×5 + 3×3 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3.) ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 – 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4.) f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x + x + 3
= x4 + x3 – 4×2 – 4x + x + 3
= x4 + x3 – 4×2 – 3x + 3
5.) f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
– p = 35 – 43
– p = -8
p = 8
6.) x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
– 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
– 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
– 27a3 + 9a3k + 18a3 + 18a3 = 0
9a3 + 9a3k = 0
9a3k = – 9a3
k = -1
7.)cara susun
x + 5 x3 + 4×2 + 11x + 30
x3 + 5×2 –
-x2 + 11x +30
-x2 + 5x –
6x + 30
6x + 30 –
0 => sisa
8.) 2×3 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 2×3 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9.) P(x) = 2×3 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 2×3 + x2 + 7x – 6
faktor dari 2×3 + x2 + 7x – 6
= ( x – 2 )(2×2 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10.) F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = – 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
Jawab
1). X3 – 3x +6 = X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2). 45 + 33 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
45 + 33 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3). ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4). f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 23 + 33 – 62 + 22 – 4x + x + 3
= x4 + x3 – 42 – 4x + x + 3
= x4 + x3 – 42 – 3x + 3
5). f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
= p = 35 – 43
= p = -8
= p = 8
6). x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
= 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
= 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
= 27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = 9a3
= k = -1
7). cara susun
x + 5 x3 + 42 + 11x + 30
x3 + 52
-x2 + 11x +30
-x2 + 5x
6x + 30
6x + 30
0=sisa
8). 23 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 23 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9). P(x) = 23 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 23 + x2 + 7x – 6
faktor dari 23 + x2 + 7x – 6
= ( x – 2 )(22 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10). F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
1)F(-2) = (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian Cara Horner
1 0 -3 6
-2 -2 4 -2 +
1 -2 1 4 , sisanya = 4
2)F(x) = 4×5 + 3×3 + x + 4 dibagi 2x + 1
F(-1/2)= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= -1/8 – 3/8 – ½ + 4
= -4/8 – ½ + 4
= – 2/2 + 4
= 3
Pembuktian Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 , sisanya = 3
3)(x-1) = 3
(x-2) = 4
Misal sisa : ax + b
F(1)= a + b = 3 …(1)
F(2)= 2a + b = 4 …(2)
Subsitusikan a = 1 ke persamaan 2 :
2a + b = 4
2(1) + b = 4
2 + b = 4
b = 4 – 2
b = 2
jadi, a = 1 & b = 2 masukan ke persamaan sisa yaitu x + 2
4)Dik. Sisanya = (x+3) jika dibagi = (x2 – 4)
Jika dibagi = (x2 + 3x + 2) Hasil bagi = (x2 – 2x)
Dit. Tentukan persamaan f(x)…?
Dij.F(x) = pembagi . hasil bagi + sisa
= (x2 + 3x + 2) (x2 – 2x) + (x+3)
= (x+2) (x+1) . x(x-2) + x + 3
Jadi,f(x)= (x2 + 3x + 2) (x2 – 2x) + x + 3
= x4 + x3 -4×2 -3x + 3
5)F(x) = x4 + 3×3 + x2 – (p+2) + 1
(x2 – 2) = 5
F(2) = (2)4 + 3(2)3 + (2)2 – (p+2) + 1 = 35
16 + 24 + 4 – p – 2 + 1 = 35
-p + 40 + 3 = 35
-p = 35 – 43
= 8
Jadi nilai p = 8
6)F(x) = x3 + (ak+sa)x2 + 18a3
X+3a
Tentukan nilai k…?
Jawab :
Cara Horner
1 ak + 2a 0 18a3
-3a -3a -3a2 k + 3a2 9a3 k-9a3 +
1 ak-a -3a2 k + 3a2 9a3 k + 9a3
9a3 k + 9a3 = 0
9a3 k = -9a3
K= -1
Jadi nilai k = -1
7)F(x) = x3 + 4×2 + 11x + 30
Tunjukan bahwa (x+5) merupakan faktornya
Jawab :
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0 , sisanya = 0
Maka x+5 adalah faktor x3 + 4×2 + 11x + 30
8)F(x) = 2×3 – x2 – 7x + 6
Tentukan faktornya!
Jawab :
Jika semua koefisien ditambahkan dan hasilnya adalah 0 maka angka 1 merupakan akarnya
Cara Horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktornya adalah = (2×2 + x-6) (x-1) = (2x-3) (x+2) (x-1)
9)Dik (x-2) merupakan faktor dari p(x) = 2×3 + x2 + ax – 6
Jawab:
P(2) = 2(2)3 + (2)2 +2a – 6
16 + 4 + 2a – 6 = 0
14 + 2a = 0
2a = -14
a=-7
disubsitusikan a= -7 ke persamaan p(x) = 2×3 + x2 + ax – 6
2×3 + x2 + 7x – 6
(x-2) (2×2 + 5x + 3)
(x-2) (2x+3) (x+1)
Jadi faktor lainnya (x-2) (2x+3) (x+1)
10)F(x) = x3 – ax2 + bx – 2
(x-1) => x = 1 sisanya 0
(x+2) => x= -2 sisanya – 36
Tentukan a + b …?
Jawab :
Cara Horner
1 –a b -2
1 1 –a + 1 –a+1 b +
1 –a + 1 –a + 1 + b 0
-2 a + 1 + b = 0
-a + b= 1 …. (1)
Cara Horner
1 –a b -2
2 -2 2a + 4 -4a -8 -2b +
1 –a -2 2a + 4 +b -36
-2 -4a-8-2b = -36
-4a -2b = -26
Disubsitusikan a = 4 ke persamaan 1
2a + b = 13 ….(2) -4+b = 1
-a+b = 1 …. (1) b = 5
2a + b = 13 ….(2) jadi a + b
-3a = -12 => a = 4 4+5 = 9
NADIFA ALIKA PUTRI
5611A3
Jawaban :
1) F(-2) = (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 +
1 -2 1 4 sisa = 4
2) F(x) = 4×5 +3×3 + X + 4 dibagi 2x + 1
F(-1/2) = 4(-1/2)5 + 3(-1/2)3 + (-1/2)+4
= -1/8 – 3/8 – ½ + 4
= -4/8 – ½ = 4
= -2/2 + 4
= 3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisa = 3
3) (X-1) = 3
(X-2) = 4
Misal sisa: ax + b
F(1) = a + b = 3 …….(1)
F(2) = 2a + b = 4 – ………(2)
a = 1
substitusikan a=1 ke persamaan 2
1+b=3
b=2
masukan a=1 dan b=2 ke persamaan sisa
Jadi sisanya adalah x + 2
4) Sisanya = (x + 3) jika dibagi (x2 – 4) sedangkan saat dibagi x2 + 3x + 2 memiliki hasil bagi (x2 – 2x), tentukan persamaan f(x)nya.
Penyelesaian:
F(x) = pembagi x hasil bagi + sisa
(x2 + 3x + 2) (x2 – 2x) + x+3
(x + 2) (x + 1) x(x-2) + X + 3
Jadi f(x) = (x2 + 3x + 2) (x2 – 2x) + x + 3
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x+x+3
= x4 + x3 – 4×2 – 3x+3
5) F(x) = x4 +3×3 +x2 – (P+x) + 1
(x-2)=5
Penyelesaian:
F(2) = (2)4 + 3(2)3 + (2)2 – (P+2) + 1 = 35
16 + 24 + 4-P-2+1=35
-P+40+3=35;
-P= 35 – 43
P = 8
Jadi nilai P = 8
6) X3 + (ak + 2a) x2 + 18a3 = (x + 3a)
= -3a3 + (ak + 2a) (-3a2) + 18a3 = -3a + 3a
= -27a3 + (ak +2a) 9a2 + 18a3 = 0
= -27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = -9a3
= k = -1
7) F(x) = x3 + 4×2 +11x+30
Tunjukan bahwa (x+5) merupakan faktornya.
Penyelesaian:
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karena sisanya = 0, maka x+5 merupakan faktor x3 +4×2 +11x+30
8) P(x) = 2×3 –x2 -7x+6
Tentukan faktor faktornya.
Penyelesaian:
Jika semua koefisien ditambahkan dan hasilnya adalah 0 maka angka 1 merupakan akarnya
Cara Horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah = (2×2 + x-6) (X-1)
= (2x-3) (x+2) (x-1)
9) Dik (x-2) merupakan faktor dari P(x)= 2×3 + x2 + ax-6
Penyelesaian:
P(2) = 2(2)3 + (2)2 + 2a – 6
16 + 4 + 2a – 6 = 0
14 + 2a = 0
2a = -14
a = -7
substitusikan a= -7 ke persamaan P(x) = 2×3 + x2 + ax – 6
2×3 + X2 + 7x – 6
(x-2) (2×2 + 5x + 3)
(x-2) (2x + 3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x + 3) (x+1)
10) F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x-2) bersisa -36, maka nilai a+b…
x-1 = 0
x = 1
Substitusikan :
F(1) = (1) – a (1) + b(1) – 2 = 0
1 – a + b – 1 = 0
-a + b – 1 = 0
-a + b = 1 …….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F(-2) = (-2)3 – a(-2)2 + b(-2) = -36
-8 – a4 – 2b – 2 = -36
-4a – 2b = -36 + 10
-4a – 2b = -26 …..pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b = 1 | x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1 = -4a – 2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a = 4
jadi, a+b = 4+5 = 9
ada yg mau ngasih komen..?silahkan dikomen aja
Yang no.2 seharusnya
f(-1/2)=4(-1/2)5+3(-1/2)3+(-1/2)+4
=-1/8-3/8-1/2+4
=-4/8-1/2+4
=-1/2-1/2+4
=-1+4
=3
NADIFA ALIKA PUTRI
5611A3
Jawaban :
1)F(-2) = (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 +
1 -2 1 4 sisa = 4
2)F(x) = 4×5 +3×3 + X + 4 dibagi 2x + 1
F(-1/2) = 4(-1/2)5 + 3(-1/2)3 + (-1/2)+4
= -1/8 – 3/8 – ½ + 4
= -4/8 – ½ = 4
= -2/2 + 4
= 3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisa = 3
3)(X-1) = 3
(X-2) = 4
Misal sisa: ax + b
F(1) = a + b = 3 …….(1)
F(2) = 2a + b = 4 – ………(2)
a = 1
substitusikan a=1 ke persamaan 2
1+b=3
b=2
masukan a=1 dan b=2 ke persamaan sisa
Jadi sisanya adalah x + 2
4)Sisanya = (x + 3) jika dibagi (x2 – 4) sedangkan saat dibagi x2 + 3x + 2 memiliki hasil bagi (x2 – 2x), tentukan persamaan f(x)nya.
Penyelesaian:
F(x) = pembagi x hasil bagi + sisa
(x2 + 3x + 2) (x2 – 2x) + x+3
(x + 2) (x + 1) x(x-2) + X + 3
Jadi f(x) = (x2 + 3x + 2) (x2 – 2x) + x + 3
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x+x+3
= x4 + x3 – 4×2 – 3x+3
5)F(x) = x4 +3×3 +x2 – (P+x) + 1
(x-2)=5
Penyelesaian:
F(2) = (2)4 + 3(2)3 + (2)2 – (P+2) + 1 = 35
16 + 24 + 4-P-2+1=35
-P+40+3=35;
-P= 35 – 43
P = 8
Jadi nilai P = 8
6)X3 + (ak + 2a) x2 + 18a3 = (x + 3a)
= -3a3 + (ak + 2a) (-3a2) + 18a3 = -3a + 3a
= -27a3 + (ak +2a) 9a2 + 18a3 = 0
= -27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = -9a3
= k = -1
7)F(x) = x3 + 4×2 +11x+30
Tunjukan bahwa (x+5) merupakan faktornya.
Penyelesaian:
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karena sisanya = 0, maka x+5 merupakan faktor x3 +4×2 +11x+30
8)P(x) = 2×3 –x2 -7x+6
Tentukan faktor faktornya.
Penyelesaian:
Jika semua koefisien ditambahkan dan hasilnya adalah 0 maka angka 1 merupakan akarnya
Cara Horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah = (2×2 + x-6) (X-1)
= (2x-3) (x+2) (x-1)
9)Dik (x-2) merupakan faktor dari P(x)= 2×3 + x2 + ax-6
Penyelesaian:
P(2) = 2(2)3 + (2)2 + 2a – 6
16 + 4 + 2a – 6 = 0
14 + 2a = 0
2a = -14
a = -7
substitusikan a= -7 ke persamaan P(x) = 2×3 + x2 + ax – 6
2×3 + X2 + 7x – 6
(x-2) (2×2 + 5x + 3)
(x-2) (2x + 3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x + 3) (x+1)
10)F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x-2) bersisa -36, maka nilai a+b…
x-1 = 0
x = 1
Substitusikan :
F(1) = (1) – a (1) + b(1) – 2 = 0
1 – a + b – 1 = 0
-a + b – 1 = 0
-a + b = 1 …….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F(-2) = (-2)3 – a(-2)2 + b(-2) = -36
-8 – a4 – 2b – 2 = -36
-4a – 2b = -36 + 10
-4a – 2b = -26 …..pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b = 1 | x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1 = -4a – 2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a = 4
jadi, a+b = 4+5 = 9
Bagus… ada yang mau kasih komentar…? silahkan…
CEMPAKA PUTRI DEWANTI
5611A3
Jawaban
1. X3 – 3x +6 =
X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2. 4×5 + 3×3 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
4×5 + 3×3 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3. ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 – 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4. f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x + x + 3
= x4 + x3 – 4×2 – 4x + x + 3
= x4 + x3 – 4×2 – 3x + 3
5. f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
= – p = 35 – 43
= – p = -8
= p = 8
6. x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
= – 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
= – 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
= – 27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = – 9a3
= k = -1
7. cara susun
x + 5 x3 + 4×2 + 11x + 30
x3 + 5×2 –
-x2 + 11x +30
-x2 + 5x –
6x + 30
6x + 30 –
0 => sisa
8. 2×3 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 2×3 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9. P(x) = 2×3 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 2×3 + x2 + 7x – 6
faktor dari 2×3 + x2 + 7x – 6
= ( x – 2 )(2×2 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10. F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = – 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
lain kali Nulis CEMPAKA PUTRI DEWANTI 5611A3, langsung di tempat nama aja, tapi kalau sudah terlanjur ndak apa-apa…
YUFLIHA SYIFANDINI
5611A3
Jawaban
1). X3 – 3x +6 =
X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2). 4×5 + 3×3 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
4×5 + 3×3 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3). ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 – 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4). f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x + x + 3
= x4 + x3 – 4×2 – 4x + x + 3
= x4 + x3 – 4×2 – 3x + 3
5). f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
= – p = 35 – 43
= – p = -8
= p = 8
6). x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
= – 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
= – 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
= – 27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = – 9a3
= k = -1
7). cara susun
x + 5 x3 + 4×2 + 11x + 30
x3 + 5×2 –
-x2 + 11x +30
-x2 + 5x –
6x + 30
6x + 30 –
0 => sisa
8). 2×3 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 2×3 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9). P(x) = 2×3 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 2×3 + x2 + 7x – 6
faktor dari 2×3 + x2 + 7x – 6
= ( x – 2 )(2×2 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10). F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = – 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
Ok, jawaban sudah bapak cek, lain kali Nulis YUFLIHA SYIFANDINI 5611A3, langsung di tempat nama aja, tapi kalau sudah terlanjur ndak apa-apa…
AL SYIFA RIDWAN FIRDAUS
5611A3
Jawaban
1). X3 – 3x +6 =
X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2). 4×5 + 3×3 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
4×5 + 3×3 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3). ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 – 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4). f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x + x + 3
= x4 + x3 – 4×2 – 4x + x + 3
= x4 + x3 – 4×2 – 3x + 3
5). f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
= – p = 35 – 43
= – p = -8
= p = 8
6). x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
= – 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
= – 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
= – 27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = – 9a3
= k = -1
7). cara susun
x + 5 x3 + 4×2 + 11x + 30
x3 + 5×2 –
-x2 + 11x +30
-x2 + 5x –
6x + 30
6x + 30 –
0 => sisa
8). 2×3 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 2×3 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9). P(x) = 2×3 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 2×3 + x2 + 7x – 6
faktor dari 2×3 + x2 + 7x – 6
= ( x – 2 )(2×2 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10). F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = – 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
jawaban sudah bapak cek, Lain kali Nulis AL SYIFA RIDWAN FIRDAUS 5611A3, langsung di tempat nama aja, tapi kalau sudah terlanjur ndak apa-apa…
CEMPAKA PUTRI DEWANTI
5611A3
Jawaban
1. X3 – 3x +6 =
X+2
X + 2 = 0
X = -2
Substitusikan :
X3 – 3x + 6
= (-2)3 – 3(-2) + 6
= -8 + 6 + 6
= 4
Pembuktian, menggunakan aturan horner :
-2 1 0 -3 6
-2 4 -2 (+)
1 -2 1 4
Terbukti bahwa sisanya adalah 4
2. 4×5 + 3×3 + x + 4 =
2x + 1
2x + 1 = 0
2x = -1
X= -1/2
Substitusikan :
4×5 + 3×3 + x + 4
= 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= 3
Pembuktian, menggunakan aturan horner :
-1/2 4 0 3 0 1 4
-2 1 -2 1 -1 (+)
4 -2 4 -2 2 3
Terbukti bahwa sisanya adalah 3
3. ( x – 1 ) = 3
f( 1 ) = 3
( x – 2 ) = 4
f( 2 ) = 4
( x2 – 3x + 2 ) = ( x – 1 )
f ( 2 ) – f ( 1 ) x + 2f ( 1 ) – 1 f ( 2 )
2 – 1 2 – 1
s= (4-3)/1 x+(2 .3-1 .4)/1
S=x+(6-4)/1
S=x+2
4. f( x ) = pembagi x hasil bagi + sisa
= ( x2 + 3x + 2 ) ( x2 – 2x ) + ( x + 3 )
= x4 – 2×3 + 3×3 – 6×2 + 2×2 – 4x + x + 3
= x4 + x3 – 4×2 – 4x + x + 3
= x4 + x3 – 4×2 – 3x + 3
5). f( 2 ) = 35
= 24 + 3 ( 2 )3 + 22 – ( p + 2 ) + 1 = 35
= 16 + 3 ( 8 ) + 4 – ( p + 2 ) + 1 = 35
= 16 + 24 + 4 – p – 2 + 1 = 35
= 43 – p = 35
= – p = 35 – 43
= – p = -8
= p = 8
6). x3 + ( ak + 2a ) x2 + 18a3 = ( x + 3a )
= – 3a3 + ( ak + 2a ) ( -3a2 ) + 18a3 = -3a + 3a
= – 27a3 + ( ak + 2a ) 9a2 + 18a3 = 0
= – 27a3 + 9a3k + 18a3 + 18a3 = 0
= 9a3 + 9a3k = 0
= 9a3k = – 9a3
= k = -1
7). cara susun
x + 5 x3 + 4×2 + 11x + 30
x3 + 5×2 –
-x2 + 11x +30
-x2 + 5x –
6x + 30
6x + 30 –
0 => sisa
8). 2×3 – x2 – 7x + 6 = ( x + 2 )(2x – 3)(x + 1)
Jadi , faktor-faktor dari 2×3 – x2 – 7x + 6 adalah
( x + 2)(2x – 3)(x + 1)
9). P(x) = 2×3 + x2 +ax – 6
P(2) = 2(2)3 + 22 +a(2) – 6
= 16 + 4 + 2a – 6 = 0
2a = -14
a = -7
persamaannya : 2×3 + x2 + 7x – 6
faktor dari 2×3 + x2 + 7x – 6
= ( x – 2 )(2×2 + 5x + 3 )
= ( x – 2 )( 2x + 3 )( x + 1 )
Jadi , faktor lain dari persamaan di atas adalah
( 2x + 3 )( x + 1)
10. F(x) = x3 – ax2 + bx – 2, mempunyai faktor x – 1 jika dibagi oleh (x – 2) bersisa – 36, maka nilai a+b….
x – 1 = 0
x = 1
substitusikan :
f (1) = (1) – a (1) + b (1) – 2 = 0
1 – a + b – 2 = 0
-a + b – 1 = 0
-a + b = 1……….pers (1)
X + 2 = 0
X = -2
Substitusikan :
F (-2) = (-2)3 – a(-2)2 + b (-2) = -36
-8 – a4 – 2b – 2 = – 36
-4a – 2b = -36 + 10
-4a – 2b = -26……….pers (2)
Eliminasi persamaan 1 dan 2 :
-a + b =1 |x 4 = -4a + 4b = 4
-4a – 2b = -26 |x 1= -4a -2b = -26 –
6b = 30
b = 5
-a + b = 1
-a + 5 = 1
-a = -4
a= 4
Membuat namanya lain kali CEMPAKA PUTRI DEWANTI 5611A3, yang sekarang ndak apa-apa…jawabannya sudah bapak cek
1. Tentukan teorema sisa x3 – 3x + 6 dibagi dengan (x + 2). Buktikan !
Penyelesaian :
X + 2 = 0
X = -2
F (x) = x3 – 3x + 6
F (-2) = (-2)3 – 3 (-2) = 6
= -8 + 6 + 6
= 4
Dibuktikan dengan cara horner
pembagi -2 dibagi dengan 1 0 -3 6
-2 4 -2 +
hasilnya 1 -2 1 4 , 4 itu sisanya
2. Tentukan sisa pembagian f (x) = 4×5 + 3×3 + x + 4 dibagi (2x – 1). Buktikan !
2x + 1 = 0
2x = -1
X = -1/2
F (x) = 4×5 + 3×3 + x + 4
F (-1/2) = 4(-1/2)5 + 3(-1/2)3 + (-1/2) + 4
= -1/8 + (-3/8) + 7/2
= -4/8 + 7/2 = 3
Pembuktian dengan cara horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
hasilnya 4 -2 4 -2 2 3
sisanya itu 3
3. suku banyak f (x) jika dibagi (x-1) sisanya 3, jika dibagi (x-2) sisanya 4, jika f(x) dibagi dengan (x2 – 3x + 2). maka tentukan sisanya
penyelesaian :
(x-1) = 3
(x-2) = 4
F (1) = a + b = 3
F (2) = 2a + b = 4 _
a = 1
1 + b = 3
b = 2
jadi, ax + b = x + 2
4. Suku banyak f(x) memiliki sisa ( x+3) jika dibagi (x2-2x). Sedangkan saat dibagi (x2 + 3x + 2) memiliki hasil bagi (x2 – 2x). Tentukan persamaan f(x) …
Penyelesaiannya :
( x2 – 4 ) -> ( x – 2 ) (x + 2 ) sisa ( x + 3)=> difaktorkan
(x2 + 3x + 2) -> (x + 1) (x + 2) sisa x2 – 2x => difaktorkan
F (2) => 2a + b = 5
F (-2) => -2ab + b = 8 –
Hasil 4a = -3
A = -3/4
2a + b = 5
2 (-3/4) + b = 5
B = 5 + 3/2
B = 10 + 3 per 2
= 13/2
=> 3/4 x + 13/2 y
5. Suku banyak f(x) = x4 + 3×2 + x2 – (p+1) x + 1 dibagi dengan x-2 memberikan sisa = 35. Tentukan nilai p…
Penyelesaian :
F (x) = x4 + 3×2 + x2 – (p+1) x + 1 dibagi x – 2 bersisa 35 => x = 2 , f (2) = 35
F (x) = x4 + 3×2 + x2 – ( px + p + x + 1)
F (x) = x4 + 3×2 + x2 – px – p – x – 1
35 = 2^4 + 3(2)^2 + 2^2 – 2p – p – 2 – 1
35 = 16 + 12 + 4 – 3p – 3
35 = -3p + 29
35 – 29 = -3p
6 = -3p
P = 6/-3 = -2
6. Tentukan nilai k sehingga ( x + 3a) merupakan faktor x3 + (ak + 2a) x2 + 18a3 …
Penyelesaian :
( x + 3a ) faktor dari x3 + (ak + 2a) x2 + 18a3 => x = 3a
(3a)^3 + ( ak + 2a ) (3a)^3 + 18a^3
27a^3 + (ak + 2a) 9a^2 + 18a^3
27a^3 + 9a^3k + 18a^3 + 18a^3
9a^3 + 63a^3
9a^3 ( k + 7 ) => k= -7
9a^3 = 0
A^3 = 0
A= 0
7. Tunjukkan bahwa (x+5) adalah faktor dari x3+4×2+11x+30
Penyelesaian:
1 4 11 30
-5 -5 5 -30 –
1 -1 16 0
Karna sisanya= 0, maka x+5 merupakan faktor x3+4×2+11x+30
FEBIANI BELLA RIZQITA 5611A3
Bagus jawabannya, Namanya lain kali membuatnya FEBIANI BELLA RIZQITA 5611A3,…biar bapak mudah liat di daftar nilainya…
JAWABAN
1. f(-2)=(-2)3 -3(-2)+6
=-8+6+6
=4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 ⁺
1 -2 1 4 sisa = 4
2. f(x)=4×5+3×3+x+4 dibagi 2x+1
f(-1/2)= 4(-1/2)5 +3(-1/2)3 +(-1/2)+4
= -1/8-3/8-1/2+4
= -4/8-1/2=4
= -2/2+4
=3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisa = 3
3. (x-1)=3
(x-2)=4
Misal sisa: ax+b
F(1)= a+b=3 …….1
F(2)=2a+b=4 – …….2
a=1
substitusikan a=1 ke persamaan 2
1+b=3
b=2
masukan a=1 & b=2 ke persamaan sisa
jadi sisanya adalah x+2
4. sisanya= (x+3) jika dibagi (x2-4) sedangkan saat dibagi x2 +3x+2 memiliki hasil bagi (x2 -2x), tentukan persamaan f(x)nya
Jawaban :
F(x)= pembagi x hasil bagi + sisa
(x2 +3x+2) (x2 -2x) + x+3
(x+2) (x+1) x(x-2) +x+3
Jadi f(x)= (x2 +3x+2) (x2 -2x) +x+3
= x4 -2×3 +3×3 -6×2 +2×2 -4x+x+3
= x4 +x3 -4×2 -3x+3
5. f(x)= x4 +3×3 +x2 -(P+x)+1
(x-2)=5
Jawaban :
F(2)= (2)4 +3(2)3 +(2)2 -(P+2)+1=35
16+24+4-P-2+1=35
-P+40+3=35
-P=35-43
P=8
jadi nilai P=8
6. f(x)= x3 +(ak+sa)x2 +18a3
X+3a
Tentukan nilai k…?
Jawaban :
Cara Horner
1 ak+2a 0 18a3
-3a -3a -3a2 k+3a2 9a3 k-9a3 +
1 ak-a -3a2 k+3a2 9a3 k+9a3
9a3 k+9a3=0
9a3 k=-9a3
k= -1
jadi nilai k =-1
7. f(x)= x3 +4×2 +11x+30
Tunjukan bahwa (x+5) merupakan faktornya
Jawaban :
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karna sisanya =0, maka x+5 merupakan faktor x3 +4×2 +11x+30
8. P(x)= 2×3 -x2 -7x+6
Tentukan faktor faktornya
Jawaban :
Jika semua koefisien ditambahlan dan hasilnya adalah 0 makan angka 1 merupakan akarnya
Cara horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah= (2×2 +x-6) (x-1)
= (2x-3) (x+2) (x-1)
9. Dik (x-2) merupakan faktor dari P(x)= 2×3 +x2 +ax-6
Jawaban:
P(2)= 2(2)3 +(2)2 +2a-6
16+4+2a-6=0
14+2a=0
2a=-14
a=-7
substitusikan a=-7 ke persamaan P(x)= 2×3 +x2 +ax-6
2×3 +x2 +7x-6
(x-2) (2×2 +5x+3)
(x-2) (2x+3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x+3) (x+1)
10. f(x)= x3-ax2+bx-2
(x-1)=> x=1 sisanya 0
(x+2)=> x=-2 sisanya -36
Tentukan a+b=…?
Jawaban :
Cara Horner
1 -a b -2
1 1 -a+1 -a+1+b +
1 -a+1 -a+1+b 0
-2-a+1+b=0
-a+b=1 ……1
Cara Horner
1 -a b -2
2 -2 2a+4 -4a-8-2b +
1 -a-2 2a+4+b -36
-2-4a-8-2b=-36
-4a-2b=-26
:2
2a+b=13 ……2
-a+b=1 ……1
2a+b=13 – ……2
-3a =-12 => a=4
substitusikan a=4 ke persamaan1
4+b=1
b=5
jadi a+b
4+5=9
YULIA LESTARI
5611A3
Yupps,…jawaban sudah bapak cek…ada yang mau mengoreksi silahkan,…lain kali untuk nama membuatnya YULIA LESTARI 5611A3 nulisnya dibagian nama, jadi bapak ngoreksinya lebih cepat,…yang sekarang ndak apa-apa
JAWABAN
1) f(-2)=(-2)3 -3(-2)+6
=-8+6+6
=4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 ⁺
1 -2 1 4 sisanya=4
2) f(x)=4×5+3×3+x+4 dibagi 2x+1
f(-1/2)= 4(-1/2)5 +3(-1/2)3 +(-1/2)+4
= -1/8-3/8-1/2+4
= -4/8-1/2=4
= -2/2+4
=3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisanya =3
3) (x-1)=3
(x-2)=4
Misal sisa: ax+b
F(1)= a+b=3 …….1
F(2)=2a+b=4 – …….2
a=1
substitusikan a=1 ke pers2
1+b=3
b=2
masukan a=1 & b=2 ke persamaan sisa
jadi sisanya adalah x+2
4) sisanya= (x+3) jika dibagi (x2-4) sedangkan saat dibagi x2 +3x+2 memiliki hasil bagi (x2 -2x), tentukan persamaan f(x)nya
Jawabannya:
F(x)= pembagi x hasil bagi + sisa
(x2 +3x+2) (x2 -2x) + x+3
(x+2) (x+1) x(x-2) +x+3
Jadi f(x)= (x2 +3x+2) (x2 -2x) +x+3
= x4 -2×3 +3×3 -6×2 +2×2 -4x+x+3
= x4 +x3 -4×2 -3x+3
5) f(x)= x4 +3×3 +x2 -(P+x)+1
(x-2)=5
F(2)= (2)4 +3(2)3 +(2)2 -(P+2)+1=35
16+24+4-P-2+1=35
-P+40+3=35
-P=35-43
P=8
jadi nilai P=8
6) f(x)= x3 +(ak+sa)x2 +18a3
X+3a
Tentukan nilai k
Cara Horner
1 ak+2a 0 18a3
-3a -3a -3a2 k+3a2 9a3 k-9a3 +
1 ak-a -3a2 k+3a2 9a3 k+9a3
9a3 k+9a3=0
9a3 k=-9a3
k= -1
jadi nilai k =-1
7) f(x)= x3 +4×2 +11x+30
Tunjukan bahwa (x+5) merupakan faktornya
Jawabannya
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karna sisanya =0, maka x+5 merupakan faktor x3 +4×2 +11x+30
8) P(x)= 2×3 -x2 -7x+6
Tentukan faktor faktornya
Jawabannya
Jika semua koefisien ditambahlan dan hasilnya adalah 0 makan angka 1 merupakan akarnya
Cara horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah= (2×2 +x-6) (x-1)
= (2x-3) (x+2) (x-1)
9) Dik (x-2) merupakan faktor dari P(x)= 2×3 +x2 +ax-6
Jawaban:
P(2)= 2(2)3 +(2)2 +2a-6
16+4+2a-6=0
14+2a=0
2a=-14
a=-7
substitusikan a=-7 ke persamaan P(x)= 2×3 +x2 +ax-6
2×3 +x2 +7x-6
(x-2) (2×2 +5x+3)
(x-2) (2x+3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x+3) (x+1)
10) f(x)= x3-ax2+bx-2
(x-1)=> x=1 sisanya 0
(x+2)=> x=-2 sisanya -36
Tentukan a+b=…?
Jawaban
Cara Horner
1 -a b -2
1 1 -a+1 -a+1+b +
1 -a+1 -a+1+b 0
-2-a+1+b=0
-a+b=1 ……1
Cara Horner
1 -a b -2
2 -2 2a+4 -4a-8-2b +
1 -a-2 2a+4+b -36
-2-4a-8-2b=-36
-4a-2b=-26
:2 substitusikan a=4 ke persamaan1
2a+b=13 ……2 -4+b=1
-a+b=1 ……1 b=5
2a+b=13 – ……2 jadi a+b
-3a =-12 => a=4 4+5=9
ANGGA RUSPANDI 5611A3
Lain kali membuat namanya ANGGA RUSPANDI 5611A3, biar bapak mudah untuk mencari datanya
iya pak siap
Makasih Alfadha, saya juga lagi nyari matri ini kebetulan sudah ada jawabanya thank makasih
JAWABAN
1) f(-2)=(-2)3 -3(-2)+6
=-8+6+6
=4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 ⁺
1 -2 1 4 sisanya=4
2) f(x)=4×5+3×3+x+4 dibagi 2x+1
f(-1/2)= 4(-1/2)5 +3(-1/2)3 +(-1/2)+4
= -1/8-3/8-1/2+4
= -4/8-1/2=4
= -2/2+4
=3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisanya =3
3) (x-1)=3
(x-2)=4
Misal sisa: ax+b
F(1)= a+b=3 …….1
F(2)=2a+b=4 – …….2
a=1
substitusikan a=1 ke pers2
1+b=3
b=2
masukan a=1 & b=2 ke persamaan sisa
jadi sisanya adalah x+2
4) sisanya= (x+3) jika dibagi (x2-4) sedangkan saat dibagi x2 +3x+2 memiliki hasil bagi (x2 -2x), tentukan persamaan f(x)nya
Jawabannya:
F(x)= pembagi x hasil bagi + sisa
(x2 +3x+2) (x2 -2x) + x+3
(x+2) (x+1) x(x-2) +x+3
Jadi f(x)= (x2 +3x+2) (x2 -2x) +x+3
= x4 -2×3 +3×3 -6×2 +2×2 -4x+x+3
= x4 +x3 -4×2 -3x+3
5) f(x)= x4 +3×3 +x2 -(P+x)+1
(x-2)=5
F(2)= (2)4 +3(2)3 +(2)2 -(P+2)+1=35
16+24+4-P-2+1=35
-P+40+3=35
-P=35-43
P=8
jadi nilai P=8
6) f(x)= x3 +(ak+sa)x2 +18a3
X+3a
Tentukan nilai k
Cara Horner
1 ak+2a 0 18a3
-3a -3a -3a2 k+3a2 9a3 k-9a3 +
1 ak-a -3a2 k+3a2 9a3 k+9a3
9a3 k+9a3=0
9a3 k=-9a3
k= -1
jadi nilai k =-1
7) f(x)= x3 +4×2 +11x+30
Tunjukan bahwa (x+5) merupakan faktornya
Jawabannya
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karna sisanya =0, maka x+5 merupakan faktor x3 +4×2 +11x+30
8) P(x)= 2×3 -x2 -7x+6
Tentukan faktor faktornya
Jawabannya
Jika semua koefisien ditambahlan dan hasilnya adalah 0 makan angka 1 merupakan akarnya
Cara horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah= (2×2 +x-6) (x-1)
= (2x-3) (x+2) (x-1)
9) Dik (x-2) merupakan faktor dari P(x)= 2×3 +x2 +ax-6
Jawaban:
P(2)= 2(2)3 +(2)2 +2a-6
16+4+2a-6=0
14+2a=0
2a=-14
a=-7
substitusikan a=-7 ke persamaan P(x)= 2×3 +x2 +ax-6
2×3 +x2 +7x-6
(x-2) (2×2 +5x+3)
(x-2) (2x+3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x+3) (x+1)
10) f(x)= x3-ax2+bx-2
(x-1)=> x=1 sisanya 0
(x+2)=> x=-2 sisanya -36
Tentukan a+b=…?
Jawaban
Cara Horner
1 -a b -2
1 1 -a+1 -a+1+b +
1 -a+1 -a+1+b 0
-2-a+1+b=0
-a+b=1 ……1
Cara Horner
1 -a b -2
2 -2 2a+4 -4a-8-2b +
1 -a-2 2a+4+b -36
-2-4a-8-2b=-36
-4a-2b=-26
:2 substitusikan a=4 ke persamaan1
2a+b=13 ……2 -4+b=1
-a+b=1 ……1 b=5
2a+b=13 – ……2 jadi a+b
-3a =-12 => a=4 4+5=9
ALFADHA HENRYAN.F(04)
XI MIA 3
Bagus Jawabannya,…untuk yang lain silahkan dicek,
boleh kasih komentar jawabannya Alfada atau memberikan jawaban yang lain juga bisa,
atau ada cara yang berbeda…
silahkan meneruskan dibawahnya..
Bagus,..ada yang mau kasih comen
3.) Suku banyak f(x) jika dibagi (x-1) sisanya 3 jika dibagi (x-2) sisanya 4. Jika dibagi dengan (x2-3x+2). Maka tentukan sisanya ?
Penyelesaian:
x2-3x+2= (x-1) (x-2)
x-1= 1
x-2= 2
a(1) + b = 3 => a+b = 3
a(2) + b = 4 => 2a+b= 4 –
-a= -1
a= 1
1+b = 3
b= 2
jadi, ax+b = x+2
4.) Suku banyak f(x) memiliki sisa (x+3) jika dibagi (x2-4). Sedang saat dibagi (x2 +3x+2) memiliki hasil bagi (x2 -2x). Tentukan persamaan f(x)nya ?
penyelesaian:
f(x)= pembagi x hasil bagi + sisa
(x2 +3x+2) . (x2 -2x) + (x + 3)
(x+2) (x+1) . (x-2) + x + 3
Jadi f(x)= (x2 +3x+2).(x2 -2x) + x + 3
= x4 -2×3 +3×3 -6×2 +2×2 -4x+x+3
= x4 +x3 -4×2 -3x+3
5.) Jika suku banyak f(x) = x4 +3×3 +x2-(p+1)x+1 dibagi oleh (x-2) sisanya adalah 35. Tentukan nilai p ?
Penyelesaian:
(x-2) –> x = 2
f(2) = 35
(2)4 +3(2)3 + (2)2 -(p+1)2+1 = 35
16+3(8) +4-(2p+2)+1 = 35
16+24+4-2p-2+1 = 35
43-2p = 35
-2p = 35-43
p = -8/-2
p = 4
6.) Tentukan nilai k sehingga (x+3a) merupakan faktor dari x3+(ak+2a) x2 +18a3 ?
Penyelesaian:
1 ak+2a 0 18a3
-3a -3a -3a2 k+3a2 9a3 k-9a3 –
1 ak-a -3a2 k+3a2 9a3 k+9a3
9a3 k+9a3 =0
9a3 k= -9a3
k= -1
Jadi, nilai k= -1
7.) Tunjukkan bahwa (x+5) adalah faktor dari x3 +4×2 +11x+30
Penyelesaian:
1 4 11 30
-5 -5 5 -30 –
1 -1 16 0
Karna sisanya= 0, maka x+5 merupakan faktor x3 +4×2 +11x+30
ANGGI LUTFIANSYAH (08)
XI-MIPA-3
Untuk teman yang lain agar mudah membedakan identitasnya memakai Format : NAMA KODE (Pakai huruf besar semua)..
CONTOH : ANGGI LUTFIANSYAH XI-MIPA-3 ditulis ANGGI LUTFIANSYAH 5611A3
JAWABAN
1) f(-2)=(-2)3 -3(-2)+6
=-8+6+6
=4
PEMBUKTIAN
Cara Horner
1 0 -3 6
-2 -2 4 -2 ⁺
1 -2 1 4 sisanya=4
2) f(x)=4×5+3×3+x+4 dibagi 2x+1
f(-1/2)= 4(-1/2)5 +3(-1/2)3 +(-1/2)+4
= -1/8-3/8-1/2+4
= -4/8-1/2=4
= -2/2+4
=3
PEMBUKTIAN
Cara Horner
4 0 3 0 1 4
-1/2 -2 1 -2 1 -1 +
4 -2 4 -2 2 3 sisanya =3
3) (x-1)=3
(x-2)=4
Misal sisa: ax+b
F(1)= a+b=3 …….1
F(2)=2a+b=4 – …….2
a=1
substitusikan a=1 ke pers2
1+b=3
b=2
masukan a=1 & b=2 ke persamaan sisa
jadi sisanya adalah x+2
4) sisanya= (x+3) jika dibagi (x2-4) sedangkan saat dibagi x2 +3x+2 memiliki hasil bagi (x2 -2x), tentukan persamaan f(x)nya
Jawabannya:
F(x)= pembagi x hasil bagi + sisa
(x2 +3x+2) (x2 -2x) + x+3
(x+2) (x+1) x(x-2) +x+3
Jadi f(x)= (x2 +3x+2) (x2 -2x) +x+3
= x4 -2×3 +3×3 -6×2 +2×2 -4x+x+3
= x4 +x3 -4×2 -3x+3
5) f(x)= x4 +3×3 +x2 -(P+x)+1
(x-2)=5
F(2)= (2)4 +3(2)3 +(2)2 -(P+2)+1=35
16+24+4-P-2+1=35
-P+40+3=35
-P=35-43
P=8
jadi nilai P=8
6) f(x)= x3 +(ak+sa)x2 +18a3
X+3a
Tentukan nilai k
Cara Horner
1 ak+2a 0 18a3
-3a -3a -3a2 k+3a2 9a3 k-9a3 +
1 ak-a -3a2 k+3a2 9a3 k+9a3
9a3 k+9a3=0
9a3 k=-9a3
k= -1
jadi nilai k =-1
7) f(x)= x3 +4×2 +11x+30
Tunjukan bahwa (x+5) merupakan faktornya
Jawabannya
Cara Horner
1 4 11 30
-5 -5 5 -30 +
1 -1 16 0
Karna sisanya =0, maka x+5 merupakan faktor x3 +4×2 +11x+30
8) P(x)= 2×3 -x2 -7x+6
Tentukan faktor faktornya
Jawabannya
Jika semua koefisien ditambahlan dan hasilnya adalah 0 makan angka 1 merupakan akarnya
Cara horner
2 -1 -7 6
1 2 1 -6 +
2 1 -6 0
Jadi faktor faktornya adalah= (2×2 +x-6) (x-1)
= (2x-3) (x+2) (x-1)
9) Dik (x-2) merupakan faktor dari P(x)= 2×3 +x2 +ax-6
Jawaban:
P(2)= 2(2)3 +(2)2 +2a-6
16+4+2a-6=0
14+2a=0
2a=-14
a=-7
substitusikan a=-7 ke persamaan P(x)= 2×3 +x2 +ax-6
2×3 +x2 +7x-6
(x-2) (2×2 +5x+3)
(x-2) (2x+3) (x+1)
Jadi faktor faktor lainnya (x-2) (2x+3) (x+1)
10) f(x)= x3-ax2+bx-2
(x-1)=> x=1 sisanya 0
(x+2)=> x=-2 sisanya -36
Tentukan a+b=…?
Jawaban
Cara Horner
1 -a b -2
1 1 -a+1 -a+1+b +
1 -a+1 -a+1+b 0
-2-a+1+b=0
-a+b=1 ……1
Cara Horner
1 -a b -2
2 -2 2a+4 -4a-8-2b +
1 -a-2 2a+4+b -36
-2-4a-8-2b=-36
-4a-2b=-26
:2 substitusikan a=4 ke persamaan1
2a+b=13 ……2 -4+b=1
-a+b=1 ……1 b=5
2a+b=13 – ……2 jadi a+b
-3a =-12 => a=4 4+5=9
ALFADHA HENRYAN.F(04)
XI MIA 3
1) X3-3x+6 dibagi (x-2)
X+2 = 0
X= -2
Disubsitusikan :
F(-2) = X3-3x=6
=(-2) 3- 3(-2) + 6
= -8+6+6 = 4
Dibuktikan dengan menggunakan pembagian horner:
1 -3 6
-2 1 -2 2
1 -1 4
Karena sisa pembagiannya 0 makan (x+2) merupakan factor dari X3-3x+6
2) 4×5 + 3×3 + x + 4 dibagi
2x+1
2x+1=0
X= -1/2
Disubsitusikan
4(-1/2)5 + 3(-1/2)3 + (-1/2) +4
=3
Pembuktian menggunakan pembagian secara horner
-2 -½ 4 0 3 0 1 4
-2 1 -2 1 -1
4 -2 4 -2 2 3
Karena sisa pembagiannya 3 maka (2x+1) merupakan factor dari 4×5 + 3×3 + x + 4
3) (x-1) =3
F(1) = x+y = 3 ………(1)
f(2) = 2x+y = 4 ………(2)
pers (1) dan pers (2) di eliminasi
Jadi x=1, y=3 masukan ke pers sisa nya jadi x+2
4) F(X)= (X2+3x+2)(X2-2X)+ (X-3)
= X4-2×3+3×3-6×2+2×2+4x+x+3
= x4+x3-4×2-3x=3
jadi f(x) = x4+x3-4×2-3x=3
5) f(X)= ….
f(2)=35
~24+3(2)+3+22-(p-2)+1=35
~16+24+4-p-2+1=35
~43-p=35
~ -p= 35-43
~ -p=-8
6) jika (x+3a) faktor dari x3+(ak+2a)x2+18a3
f(3)=0
Disubsitusikan
x=-3a
f(-3a)= 9a3+9ka3=0
= 9ak3=-9ak3
k=-1
jadi nilai a adalah -1
7) f(x)= x3+4×2+11x+30
(x+5) faktornya
~menggunakan metode horner
1 4 11 30
x=5 -5-5 5-30
1-1 16 0
karena sisa pembagiannya 0 maka (x+5) merupakan faktor dari x3+4×2+11x+30
8) f(x)= 2×3-x2-7x+6
~menggunakan metode horner
2 -1 -7 6
x=1 1 2 1 -6
2 1 -6 0
jadi faktor nya ialah (2x2x+x-6)(x-1)
=(2x-3)(x+2)(x-1)
9) f(x)= 2×3+x2+ax-6
faktornya (x-2)
f(x)= 2(2)3+(2)2+2a-6=0
= 14+2a=0
a= -7
disubsitusikan
2×3+x2+7x-6
=(x-2)(2×2+5x+3)
jad faktor-faktor lainnya ialah = (x-2)(2x+3)(x+1)
MEDINA AULIA 5611A1