
A. Sistem Persamaan Linear dua variabel
- Sistem persamaan linier dua variabel adalah dua persamaan linier dan dua variabel yang hanya memiliki satu titik penyelesaian.
- Sistem persamaan linear dua variabel sering disingkat SPLDV
- Bentuk umum :
a1x + b1y = c1
a2x + b2y = c2
B. Menyelesaikan Persamaan Linear dua variabel
Dalam menyelesaikan soal-soal persamaan linear dua variable ada 4 Metode ;
- Metode Subtitusi
- Metode Eliminasi
- Metode Subtitusi Eliminasi
- Metode Grafik
Metode Subtitusi
- Metode subsitusi dimulai dengan menyatakan sebuah variabel dari salah satu sistem persamaan linier dua variabel dalam variabel lain.
- Contoh : Diberikan dua persamaan 2x + y = 12 dan x − y = 3 . Tentukan nilai x dan nilai y dengan menggunakan metode substitusi!
Dari persamaan kedua:
x − y = 3
x = 3 + ySubstitusikan ke persamaan kedua:
2x + y = 12
2(3 + y) + y = 12
6 + 2y + y = 12
6 + 3y = 12
3y = 12 − 6
3y = 6
y = 6/3
y = 2 Berikutnya substitusikan nilai y yang sudah diperoleh, ke persamaan pertama atau kedua, misal diambil persamaan pertama:
x − y = 3
x − 2 = 3
x = 3 + 2
x = 5
Himpunan Penyelesaian HP:{(5, 2)}
Metode Eliminasi
- Metode eliminasi adalah cara untuk mendapatkan nilai pengganti suatu variabel melalui penghilangan variabel yang lain. Untuk mengeliminasi suatu variabel, langkah pertama yang dilakukan adalah menyamakan koefisien variabel tersebut
- Contoh : Diberikan dua persamaan linier 2x + y = 12 dan x − y = 3 . Tentukan nilai x dan nilai y dengan menggunakan metode eliminasi!
Pembahasan
Untuk menentukan nilai x, maka y kita eliminasi terlebih dahulu:
2x + y = 12
x − y = 3
______________ +
3x = 15
x = 15/3 = 5
Untuk menentukan nilai y, maka x yang kita eliminasi:
2x + y = 12 |× 1 | 2x + y = 12
x − y = 3 |× 2 | 2x − 2y = 6
____________ –
3y = 6
y = 6/3 = 2
Himpunan Penyelesaian HP:{(5, 2)}
Metode Gabungan Substitusi dan Eliminasi
- Metode Gabungan Subtitusi dan Eliminasi adalah cara untuk mendapatkan nilai pengganti suatu variabel melalui cara pengabungan antara eliminasi dan subtitusi, terlebih dahulu mengeliminasi salah satu variabel kemudian setelah didapat angkanya baru disubstitusikan kepersamaan lain.
- Contoh : Diberikan dua persamaan 2x + y = 12 dan x − y = 3 . Tentukan nilai x dan nilai y dengan menggunakan metode eliminasi yang dikombinasi dengan metode substitusi!
Pembahasan
Eliminasi,
Untuk menentukan nilai x, maka y kita eliminasi terlebih dahulu:
2x + y = 12
x − y = 3
______________ +
3x = 15
x = 15/3 = 5 Setelah nilai x ketemu, langsung disubstitusikan ke salah satu persamaan:
Subtitusi
x − y = 3
5 − y = 3
y = 5 – 3
y = 2
Himpunan Penyelesaian HP:{(5, 2)}
Metode Grafik
- Adalah metode penyelesaian SPLDV yang dilakukan dengan cara menggambar grafik dari kedua persamaan tersebut yang kemudian menentukan titik potongnya.
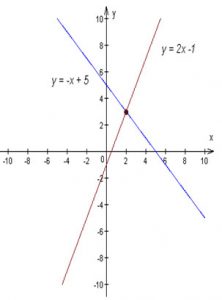
- Contoh : Selesaikan persamaan dua variabel berikut y = 2x -1, y = -x + 5 dengan menggunakan metode grafik.
Pembahasan :
Grafik garis menunjukkan himpunan penyelesaian dari masing-masing persamaan dalam sistem. Oleh karena itu, perpotongan kedua garis adalah gambar dari penyelesaian sistem. Solusi dari sistem adalah (2,3)
C. Contoh Soal dan penyelesaiannya
Diketahui sistem persamaan menggunakan metode eliminasi
3x + 7y = 1
2x – 3y = 16
Nilai x y =….
B. 6
C. –10
D. –12
E. -16
(Dari soal UN 2005)
3x + 7y = 1 |× 2| 6x + 14y = 2
2x – 3y = 16 |× 3| 6x – 9y = 48
___________ _
23y = – 46
y = – 46/23 = – 23x + 7y = 1
3x + 7(-2) = 1
3x – 14 = 1
3x = 1 + 14
3x = 15
x = 15/3
x = 5 Sehingga
xy = (-2)(5) = – 10
a. X= -2 , y = -2
b. X = 0, y = 2
c. X = 2 , y = 0
d. X = 0 , y = -2
e. X = 2 , y = 2
Soal Latihan
- Suatu sistem persaman linear dua variabel seperti berikut:
2x + 3y = 23
4x + 2y = 26
Nilai x + y =…. - Tentukan nilai dari x-y :
5y = 11 – 3x
4x = 10 – 2y
- Tentukan nilai dari x dan y :
x = 3y – 1
4x = 2y + 6

Subtitusikan x+2y=12 2x+y=12
Tentukan nilai x dan y dari kesamaan matriks berikut
[x+2 3] [10 6/2]
[-1 0] = [y+1 0 ]
x = 3y – 1 |2| 2x = 6y – 2
4x = 2y + 6 |3| 12x = 6y + 18
_______________-
-10x = -20
x = -20/-10
x = 2
x = 3y – 1
2 = 3y – 1
3y = 2 + 1
y = 3/3
y = 1
x = 2
y = 1
5y = 11 – 3x 11 = 3x + 5y
4x = 10 – 2y 10 = 4x + 2y
3x + 5y = 11 |4| 12x + 20y = 44
4x + 2y = 10 |3| 12x + 6y = 30
________________-
14y = 14
y = 14/14
y = 1
4x = 10 – 2y
4x = 10 – 2(1)
4x = 10 – 2
4x = 8
x = 8/4
x = 2
x – y = ….
2 – 1 = 1
2x + 3y = 23
4x + 2y = 26
2x + 3y = 23 |2| 4x + 6y = 46
4x + 2y = 26 |1| 4x + 2y = 26
_____________ –
4y = 20
y = 20/4
y = 5
2x + 3y = 23
2x + 3(5) = 23
2x + 15 = 23
2x = 23 – 15
2x = 8
x = 8/2
x = 4
x + y = ….
4 + 5 = 9
Jawaban nomor 1
2x+3y=23 |2| 4x+6y =46 2x+3y=23
4x+2y=26 |3| 12x+6y=78 2.(4)+3y=23
-8x = -32 8+3y =23
x = 4 3y =23-8
3y =15
y =5
Jadi nilai x+y= 4+5=9
Jawaban nomor 2
5y=11-3x 5y+3x=11 |2| 10y+6x =22
4x=10-2y 2y+4x=5 |5| 10y+20x=50
-14x = -28
X= 2
2y+4x=10
2y+4.(2)=10
2y+8 =10
2y =10-8
2y=2
y=1
Jadi nilai x-y yaitu 2-1=1
Jawaban nomor 3
x=3y-1 x-3y=-1 |4| 4x-12y=-4
4x=2y+6 4x-2y=6 |1| 4x-2y =6
-10y=-10
y=1
4x-2y=6
4x-2.(1)=6
4x-2 =6
4x=6+2
4x=8
x=2
Jadi,nilai x dan y adalah x=2 dan y=1
soal no 1
2X + 3Y = 23 … 1
4X + 2Y = 26 … 2
CARA MENYELESAIKANNYA PERASAMAAN PERTAMA DAN KEDUA HARUS MENGGUNAKAN METODE ELIMINASI
2X + 3Y = 23 X2 => 4X + 6Y = 46
4X + 2Y = 26 X1 => 4X + 2Y = 26
————— –
4Y = 20
Y = 4
2X + 3Y = 23 X2 => 4X + 6Y = 46
4X + 2Y = 26 X3 => 12X + 6Y = 78
——————— –
-8X = -32
X = 4
JADI NILAI X + Y ADALAH 4 + 5 = 9
SOAL NO 3
X = 3Y – 1
4X = 2Y + 6
CARA MENYELESAIKANNYA PERSAMAAN PERTAMA DAN KEDUA HARUS MENGGUNAKAN METODE CAMPURAN
X – 3Y = 1 X4 => 4X – 12Y = 4
4X – 2Y = -6 X1 => 4X – 2Y = -6
——————– –
-10Y = 10
Y= -1
DISUBSITUSIKAN
X – 3Y = 1 => X = 1 +3Y
4X-2Y = -6
4 (1+3Y) – 2Y =-6
4 + 12Y – 2Y = -6
4 – 10Y = -6
-10Y = -6 -4
-10Y = -10
Y = -10 : -10
Y = -1
NILAI X DAN Y
X= 1
Y= -1
maaf pak saya salah hitung yang,
X -3y=1
4x -2y=-6
-2y=-6-4x
————- :-2
y= 3+2x
x-3y=1
x-3(3+2x)=1
x-9-6x=1
-5x=1+9
-5x=10
x=2
Jawaban no 1
2x + 3y = 23 x2 4x + 6y = 46
4x + 2y = 26 x1 4x + 2y = 26
______________ –
4y = 20
y = 5
2x + 3(5)= 23
2x+ 15 = 23
2x = 8
x = 4
nilai x + y adalah 4 + 5 = 9
jawaban soal no 2
Pindahkan saja
3x + 5y = 11 x4 12x + 20y = 44
4x + 2y = 10 x3 12x + 6y = 30
________________ –
14y = 14
y = 1
3x + 5(1)= 11
3x + 5 = 11
3x=6
x=2
jadi x-y = 2-1 =1
jawaban soal no 3
pindahkan saja
x – 3y = -1 x4 4x – 12y = -4
4x – 2y = 6 x1 4x – 2y = 6
__________-
-10y = -10
y = 1
x – 3(1) = -1
x – 3 = -1
x = 2
jadi x = 2 dan y = 1
hmm maaf bukannya X= 3Y – 1 kalau dipindah ruas kan menjadi x – 3y = 1 ya , itu sih menurut saya heheh:v
tidak, karna -1 itu posisinya tetap, yang pindah hanya 3y