
A. Menjumlah dan Mengurangkan Bentuk Akar
Bentuk-bentuk akar yang dapat dijumlahkan atau dikurangkan adalah bentuk-bentuk yang sejenis yakni yang sama pangkat akamya dan sama bilangan di bawah tanda akamya.
Contoh :
a. 3√5 + √5 = (3+1)√5 = 4√5
b. 3√5 – √5 = (3-1)√5 = 2√5
c. 3√2 – √8 + √32 = 3√2 + 2√2 + 4√2 = (3 + 2 + 4)√2 = 9√2
B. Hasil Kali Bentuk Akar
Contoh
a. x
=
b.
c.
C. Latihan Soal dan Pembahasan
Soal No. 01
Sederhanakanlah bentuk berikut ini:
a). 2√5 + 3√5 – 4√5
b). 4√7 – 3√7 + 2√7
Pembahasan
a). 2√5 + 3√5 – 4√5 = (2 + 3 – 4)√5 = (5 – 4)√5 = √5
b). 4√7 – 3√7 + 2√7 = (4 – 3 + 2)√7 = (1 + 2)√7 = 3√7
Soal No. 02
Tentukan hasil dari operasi berikut:
a).√8 x √12
b). 2√3 x 5√2
Pembahasan
a).√8 x √12 = √(8 x 12) = √96 = √(16 x 6) = 4√6
b). 2√3 x 5√2 = (2 x 5) x √3 x √2 = (2 x 5) x √(3 x 2) = 10 x √6 = 10√6
Soal No. 03
Selesaikan operasi bilangan berikut ini:
a).√3 x 3√2 + 5√6
b).2(√36 : √9) – (2√12 : √3)
Pembahasan
Sebelum mengerjakan operasi campuran, terlebih dahulu kita fahami urutan operasi hitung berikut ini: Yang menjadi prioritas untuk didahulukan dalam operasi hitung adalah bilangan-bilangan yang ada di dalam tanda kurung. Apabila tidak ada tanda kurungnya maka:
a. Pangkat dan akar sama kuat.
b. Kali dan bagi sama kuat.
c. Tambah dan kurang sama kuat
d. Kali dan bagi lebih kuat daripada tambah dan kurang.
maka :
a).√3 x 3√2 + 5√6 = (√3 x 3 x √2) + 5√6 = (3 x √6) + 5√6 = 3√6 + 5√6 = 8√6
b).2(√36 : √9) – (2√12 : √3) = (2√4) – (2√4) = 0
Soal No. 04
Tentukan hasil operasi penjumlahan dan pengurangan dari soal-soal berikut dan nyatakan hasilnya dalam bentuk akar yang paling sederhana!
Soal No. 05
Tentukan hasil operasi aljabar berikut dalam bentuk yang paling sederhana!
Pembahasan


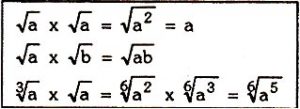
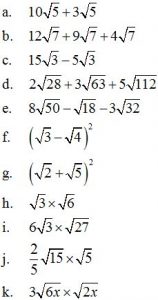


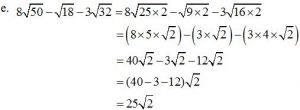
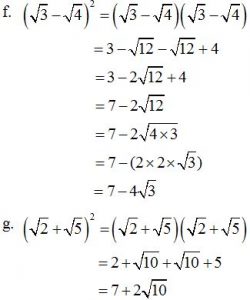
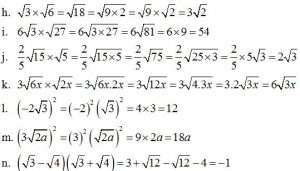

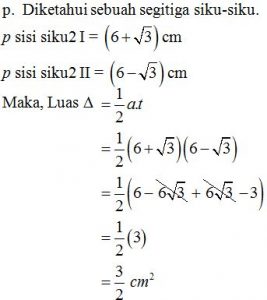
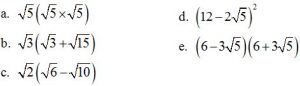
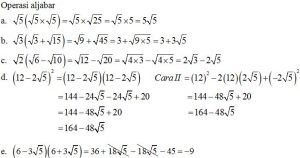
Soal matematika dasar